- #1
yrjosmiel
- 53
- 5
Something about collisions has been bothering me.
Let's say I have 2 particles with equal mass: one is moving at velocity v towards the other particle. Kinetic energy and momentum is conserved during this collision. However, I have a question: what is the acceleration of the particles during the collision? Is it infinite (since the particles suddenly change velocity in an instant)? I know it shouldn't be, or should it?
velocity-time graph of particle 1
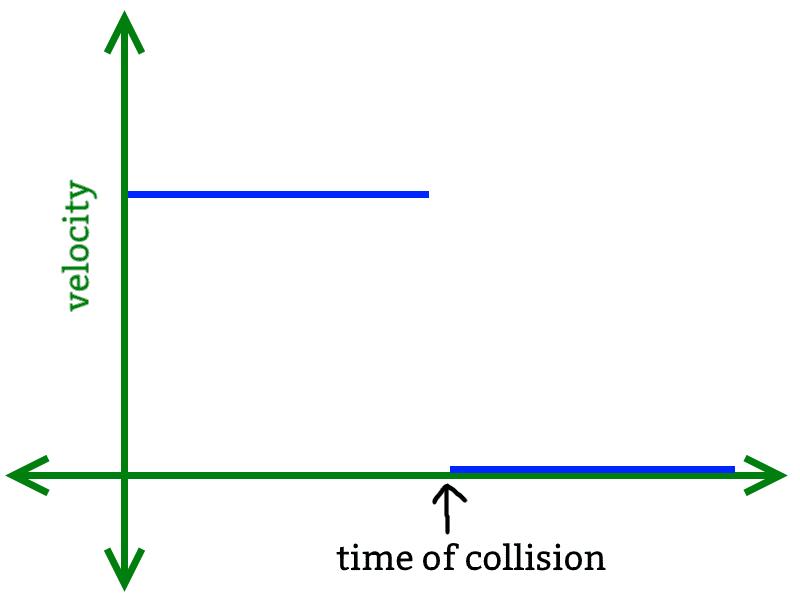
velocity-time graph of particle 2
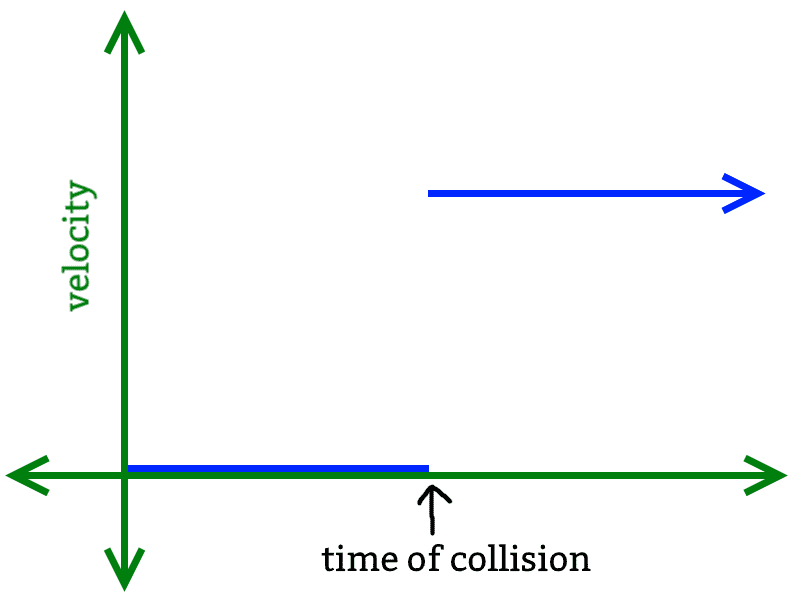
Let's say I have 2 particles with equal mass: one is moving at velocity v towards the other particle. Kinetic energy and momentum is conserved during this collision. However, I have a question: what is the acceleration of the particles during the collision? Is it infinite (since the particles suddenly change velocity in an instant)? I know it shouldn't be, or should it?
velocity-time graph of particle 1
velocity-time graph of particle 2