The Dependence of Angular Acceleration on Moment of Inertia and Mass

[TheFallen018]

Hey guys,

Forgive my ignorance on some of these things. I'm having a bit of trouble understanding the meaning of this question.

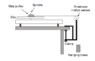
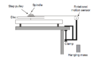
In a previous question, the angular acceleration was found to be given by α=mgr/(I+mr^2) where I is the moment of inertia for a disk.

So, question 6, I figure that we would do that by first taking the mean of the set of measured values, and then getting the uncertainty in the mean by (x_max-x_min)/2

However, I'm unsure as to how the dependence would manifest here. I can't seem to find much clear cut info, and it's just leaving me more confused. Am I correct in thinking that the mass is independent, and the angular acceleration is the dependent variable?

If so, how could a linear dependence be expected? I've thought of a few things, such as changing r without changing the mass, but these things don't seem to make sense. I think I've just confused myself to the point that these efforts are futile without external input. Thanks

 

[Cutter Ketch]

Regarding the uncertainty of the mean, it is not just the spread of the data. The spread of the data indicates how much error there was in each measurement. The mean of all those measurements is much more precise than the spread of the data. For example, if you made n measurements AGAIN you would get a similar spread in the data, and you wouldn’t expect the new mean to ever be at the extremes of the data distribution. See if your textbook mentions “deviation of the mean”.

Also, (max - min)/2 is a simplistic way to understand the uncertainty, but it isn’t the usual way for lots of good reasons. A more statistically useful definition is the standard deviation. A choice of definition of uncertainty isn’t needed for this problem, so I won’t belabor the point. However, since you mentioned it, I thought I’d let you know.

As for question 7, I don’t think we can help until we understand the previous problem better. In short we have no idea what m is. The result you state looks like maybe there is a mass m hanging under gravity from a wire that is routed over a pulley and goes to the edge of the disk applying a torque. However you also seem to have some other mass (also m?) sitting on the edge of the disk and spinning with it?

 

[tnich]

Am I correct in thinking that the mass is independent, and the angular acceleration is the dependent variable?

Yes. That's right.

Start by thinking what the equation for a linear dependence of $\alpha$ on $m$ would look like. How does α=mgr/(I+mr^2) differ from that equation? What part of that equation would have be to constant to make it look linear? Since you are trying to set up a linear dependence of $\alpha$ on $m$, you can't hold $m$ constant, but you can play with $I$ and $r$. What conditions on $I$ and $r$ would make the relationship look almost linear? (I say "almost" here, because it can't be exactly linear.)

 

[TheFallen018]

Regarding the uncertainty of the mean, it is not just the spread of the data. The spread of the data indicates how much error there was in each measurement. The mean of all those measurements is much more precise than the spread of the data. For example, if you made n measurements AGAIN you would get a similar spread in the data, and you wouldn’t expect the new mean to ever be at the extremes of the data distribution. See if your textbook mentions “deviation of the mean”.

Also, (max - min)/2 is a simplistic way to understand the uncertainty, but it isn’t the usual way for lots of good reasons. A more statistically useful definition is the standard deviation. A choice of definition of uncertainty isn’t needed for this problem, so I won’t belabor the point. However, since you mentioned it, I thought I’d let you know.

As for question 7, I don’t think we can help until we understand the previous problem better. In short we have no idea what m is. The result you state looks like maybe there is a mass m hanging under gravity from a wire that is routed over a pulley and goes to the edge of the disk applying a torque. However you also seem to have some other mass (also m?) sitting on the edge of the disk and spinning with it?

Wow, you're sharp. What you described almost exactly describes the problem presented. I'm glad you mentioned using the standard deviation, as that's what I wanted to use, but it seemed obvious, so I was second guessing myself.

Here is what the problem looks like, for more info.

The things that are assumed here is that the moment of inertia for the rotational sensor is negligible compared to the step pulley, the string doesn't slip or stretch, and at this point we are also assuming no friction. What we don't know is the radius of the step pulley, the mass or the step pulley, or the hanging mass.

Yes. That's right.

Start by thinking what the equation for a linear dependence of $\alpha$ on $m$ would look like. How does α=mgr/(I+mr^2) differ from that equation? What part of that equation would have be to constant to make it look linear? Since you are trying to set up a linear dependence of $\alpha$ on $m$, you can't hold $m$ constant, but you can play with $I$ and $r$. What conditions on $I$ and $r$ would make the relationship look almost linear? (I say "almost" here, because it can't be exactly linear.)

Am I right in thinking that an equation for linear dependence of $\alpha$ on $m$ would look like $\alpha=a/r$? In this case, a linear dependence should occur when $m>>I$. This would result in the equation breaking down to $\alpha=g/r$ if we cancel out $I$, due to it being negligible. Does that seem right? Thanks

 

[tnich]

Am I right in thinking that an equation for linear dependence of $\alpha$ on $m$ would look like $\alpha=mg/r$? In this case, a linear dependence should occur when $m>>I$. Does that seem right? Thanks

No. I was thinking of something like this $\alpha = Cm$. That would be a line with slope $C$. So for your original equation for $\alpha$ to look like that $\frac {gr} {I+mr^2}$ would have to be a constant (or approximately constant).

 

[Cutter Ketch]

Here is what the problem looks like, for more info.

So based on this picture I think your expression for angular acceleration must be wrong. It will be hard to reason question 7 starting with an incorrect expression.

 

[tnich]

So based on this picture I think your expression for angular acceleration must be wrong. It will be hard to reason question 7 starting with an incorrect expression.

I get exactly the same equation OP does for $\alpha$.

In a previous question, the angular acceleration was found to be given by α=mgr/(I+mr^2) where I is the moment of inertia for a disk.

Could you show us how you arrived at this equation, please?

 

[TheFallen018]

Here, let me link in the whole two pages. It might fill in the gaps.

https://imgur.com/a/B4KI8KM

The equation for angular acceleration is given in that file. I still tried to work it out on paper. Here's what I got.

https://imgur.com/a/aRcxV1C

No. I was thinking of something like this $\alpha = Cm$. That would be a line with slope $C$. So for your original equation for $\alpha$ to look like that $\frac {gr} {I+mr^2}$ would have to be a constant (or approximately constant).

Hmm, it seems that the only way that it would be constant is as it approaches 1. If m is an independent variable, how would this be constant?

 

[Cutter Ketch]

I get exactly the same equation OP does for αα\alpha.

Oops. My bad. Didn’t think about it hard enough. Yes, it’s correct. Please disregard.

 

[Cutter Ketch]

Hmm, it seems that the only way that it would be constant is as it approaches 1. If m is an independent variable, how would this be constant?

No, not 1. The m just has to be irrelevant. (In the thing tnich identified as C, not in the whole thing, obviously). Looking at C what would have to be true for C to not change much when you change m?

 

[TheFallen018]

No, not 1. The m just has to be irrelevant. (In the thing tnich identified as C, not in the whole thing, obviously). Looking at C what would have to be true for C to not change much when you change m?

So, C should be independent of m? I'm not sure how the m could become irrelevant though, unless there is a large disparity between I and m? I apologise that I'm missing the obvious here

 

[Cutter Ketch]

So, C should be independent of m? I'm not sure how the m could become irrelevant though, unless there is a large disparity between I and m? I apologise that I'm missing the obvious here

You aren’t missing anything. That’s the answer. Only, not just “disparity”, direction matters. Which has to be bigger? And not just m. The whole term in the denominator.