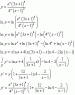The derivative using logarithmic differentiation. Is this correct?

Click For Summary
The discussion focuses on using logarithmic differentiation to find the derivative of a function. A participant questions the correctness of their solution, particularly addressing a mistake in the transition from the 5th to the 6th line regarding ln(e). They clarify that ln(e) equals 1, which simplifies their expression correctly. The final derivative calculation, resulting in d/dx(x) = 1, is confirmed as accurate. Overall, the use of logarithmic differentiation is validated in this context.
dylanhouse
Messages
42
Reaction score
0
1. Homework Statement [/b]

Find the derivative of the given function.

Homework Equations



Chain rule and logarithmic differentiation.

The Attempt at a Solution



See attached .gif. I was just wondering if this seemed correct? Thanks!
 

Attachments

  • Calculus Problem.gif
    Calculus Problem.gif
    3.5 KB · Views: 533
Physics news on Phys.org
You made a small mistake going from the 5th to the 6th line. ln(e) = ?
 
ln(e) = 1. I replaced it in the 7th line.
 
dylanhouse said:
ln(e) = 1. I replaced it in the 7th line.

I mean, xln(e) = x(1) = x right?

\frac{d}{dx} (x) = 1
 
It looks fine to me as it is.
 

Thread 'Distance between a Clock's hands when the distance is increasing most rapidly'

Question: A clock's minute hand has length 4 and its hour hand has length 3. What is the distance between the tips at the moment when it is increasing most rapidly?(Putnam Exam Question) Answer: Making assumption that both the hands moves at constant angular velocities, the answer is ## \sqrt{7} .## But don't you think this assumption is somewhat doubtful and wrong?
View full post »

Similar threads

Alternate way of differentiating x^y
  • · Replies 6 ·
Replies
6
Views
2K
Finding a definite integral from the Riemann sum
  • · Replies 2 ·
Replies
2
Views
1K
Correct Usage of Partial Derivative Symbols in PDEs
  • · Replies 10 ·
Replies
10
Views
2K
Where is ##(z+1)Ln(z)## differentiable?
  • · Replies 5 ·
Replies
5
Views
2K
How Can I Solve a Differential Equation in Physics Homework?
  • · Replies 4 ·
Replies
4
Views
1K
Problem in applying the Chain Rule
  • · Replies 3 ·
Replies
3
Views
2K
Use logarithmic differentiation to find the derivative
  • · Replies 7 ·
Replies
7
Views
4K
Solving a Derivative Problem using Chain Rule and Logarithmic Differentiation
  • · Replies 4 ·
Replies
4
Views
2K
Taylor Series Expansion Confusion
  • · Replies 6 ·
Replies
6
Views
2K
Why Is the Chain Rule Not Used in Differentiating h(x) = 3f(x) + 8g(x)?
  • · Replies 2 ·
Replies
2
Views
2K