The effect of a switch in a Laplace circuit analysis

[marsupial]

Homework Statement

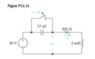
The switch in the circuit in has been closed for a long time. At the switch is opened. a) Find i₀ for t>=0 (b) find v₀ for t>=0

I don't understand the effect of the switch in the position it is in. It's acting as a short circuit, I think, so presumably the capacitor doesn't charge. But I don't understand how they have calculated the initial current. Also, for the second part of the solution, they seem to have inserted a value of 0.1 for p in the voltage near the inductor. I am not sure where they got that from either.

Homework Equations

The solution is given below, but there are a couple of things I don't understand:

The Attempt at a Solution

I really wasn't sure why they did what they did. I tried to do a voltage divider to get the voltage at v(0) but then realized it was irrelevant anyway as it acted as a short when the switch was closed so the inductor wasn't charged anyway.

I now realize where they got 0.1 from - the initial current, as the capacitor is shorted and the inductor also acts as a short, so the initial current is 0.1 (from 80/800). But I still don't understand where they got their equation from for initial current, namely: io(0−) = 20/4000 = 5 mA

 

[gneill]

With the switch closed the capacitor is effectively removed from the circuit, and "closed for a long time" means that steady state conditions will hold for the series RL circuit. That will involve some constant current.

When the switch opens the former steady-state current from t = 0^- will be maintained at t = 0⁺ by the energy stored in the inductor. There are a couple of ways to account for this stored energy in the s-domain, one of which is to represent it by a pseudo voltage with magnitude $V = IL$ where $L$ is the inductance and $I$ is the initial current.

The Wikipedia article on Laplace Transforms has a section called "s-domain equivalent circuits and impedances" which shows the alternative methods for both inductors and capacitors.

 

[marsupial]

Thank you. But how did they get the initial current of 5mA? I would have thought it was 1mA, as used in the s-domain circuit?

 

[NascentOxygen]

20/4000 must belong to a former problem, but they changed the source and resistance for this problem and forgot to fix the old equation for i_o(0⁺). That's what I'd say. It's a blunder.

 

[marsupial]

Thank you. I can stop tearing my hair out now :-)

 

[bhobba]

First a caveat - I am not an engineering guy - I did a degree in applied math. But I had an interest in electronics in my misspent youth and we did these types of problems in applied differential equations so how I would solve it may be different to an engineer.

Since the switch has been closed for a long time the capacitor is discharged and the voltage across it is zero. That is the initial condition. Now you write a differential equation for the current, noting the current through a capacitor is the differential of the voltage across it times its capacitance. Its the opposite for an inductor ie the voltage across the inductor is the differential of the current going through it times the inductance, and the resistor is of course E=I*R

We know the total voltage is 80V. This will allow you to write a differential equation for the current

80 = 1/(25*10^-6) ∫ I dt + 800*I + 4*10^-3 dI/dt.

We differentiate it to get a second order differential equation

0 = 1/(25*10^-6) I + 800*dI/dt + 4*10^-3*dI^2/dt.

You then look at initial conditions when the switch is closed. The current will be steady so there is no voltage across the inductor before the switch is open. Hence you use I = 80/800 = 1/10 to get the initial current. It will not change instantly (mathematically we assume its continuous) when closed so at t=0 (assuming that is the time the switch is opened ie switched off) it will be 1/10. We have the first initial condition. But being a second order equation you also need the derivative of the initial current. This immediately suggests we look at the inductor because its voltage involves di/dt. But since initially the voltage across the inductor is 0 we know initially di/dt = 0.

So we have a second order differential equation to solve. Hopefully you know how to solve such. But in case you do not here is the general method. Let's assume a solution is of the form e^ct. Substitute it into the equation and you end up with a quadratic equation in c - solve it and you get two possible solutions c1 and c2. So possible solutions to the differential equations are e^c1 and e^c2. However since the equation is linear A*e^c1 +B*e^c2 where A and B are arbitrary constants determined by the initial conditions is also a solution. It can be shown it is the only solution. Math guys like me may or may not depending on how the teacher feels be shown the proof. My teacher didn't bother - but I have since looked it up and you can as well if such interests you. Most engineers aren't into that sort of thing so feel free to not worry about it.

This should be enough for you to actually do it.

Thanks
Bill

 

[marsupial]

Thanks Bill, I appreciate it. We did cover solving circuits using differential equations earlier, this question was in a section of the textbook on using laplace transforms to solve it, so that's why I was focusing on that. What was mystifying me was how they got the 5mA for the current, and the effect of the short, but it seems that was a mistake, and I understand the short effect now. The laplace part I understand. But its always good to hear another perspective. I do think I prefer the laplace approach at the moment though :-)

thanks
Rebecca

 

[bhobba]

We also did Laplace in our differential equation course - its easier. Even easier is to shove it into something like Mathlab which is how such things are usually done in practice. You do a couple manually using the from the first principles method I gave, then the easier Laplace Transforms to cement the concepts like at school when adding numbers. Because of calculators there is no need to practice adding a long list of numbers, large multiplications etc - you simply do a couple and from then on leave it to the calculator.

Thanks
Bill