funmi
- 10
- 1
Why is an emf induced in straight current carrying conductor as it moves at at right angles to a uniform and constant magnetic filed. By Faraday's law, this e.m.f. is equal to dΦ/dt but I do not understand how a wire cutting a uniform magnetic field experiences a change in magnetic flux . Its area is constant and magnetic flux density is constant so the magnetic flux felt by the wire Φ=BA is constant.
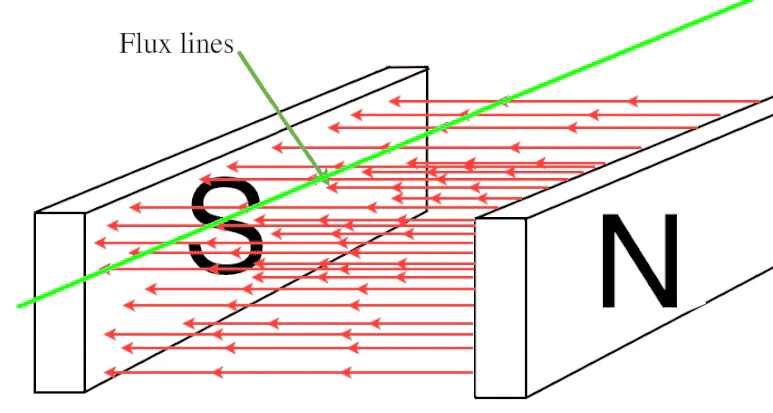
Wire(green) is moving down at right angles to the field
Wire(green) is moving down at right angles to the field
Last edited: