Asmaa Mohammad
- 182
- 7
The induced emf in a straight wire is determined by the equation (emf=Blv sinθ) where θ is the angle between the direction of the motion and the lines of the magnetic field, and frequently, I see diagrams like these explaining the phenomenon:
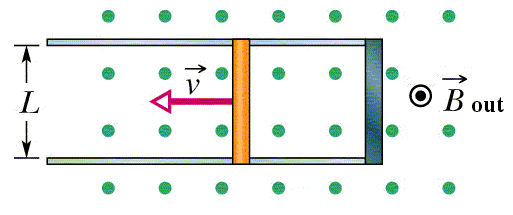
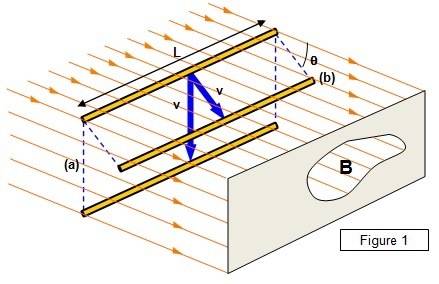
In those pictures the wire is perpendicular to the lines of the field, so it starts its motion of that state, and I was wondering what if the wire was like this:
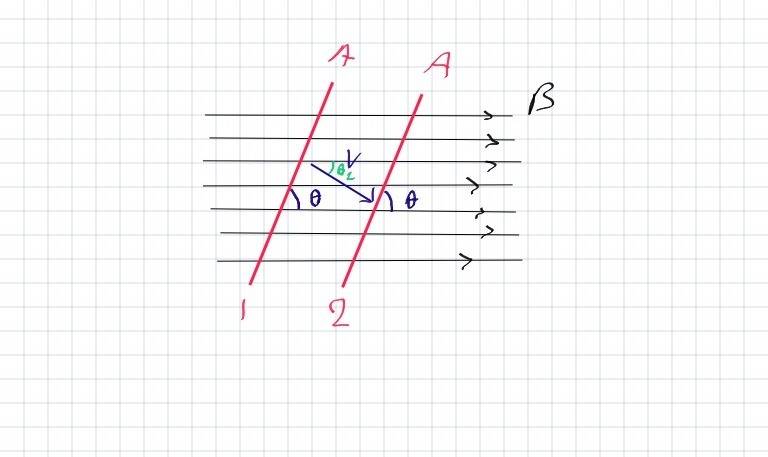
In that diagram the angle between the wire and the field is not 90 it is θ1 and the angle between the direction of the motion and the magnetic field lines is θ2.
So, in the equation (emf=Blv sinθ) which angle will be involved here? θ1 or θ2? Or θ1=θ2? And then there will be no difference.
Note: in the last diagram the wire moves from position 1 to position 2.
In those pictures the wire is perpendicular to the lines of the field, so it starts its motion of that state, and I was wondering what if the wire was like this:
In that diagram the angle between the wire and the field is not 90 it is θ1 and the angle between the direction of the motion and the magnetic field lines is θ2.
So, in the equation (emf=Blv sinθ) which angle will be involved here? θ1 or θ2? Or θ1=θ2? And then there will be no difference.
Note: in the last diagram the wire moves from position 1 to position 2.
Last edited: