The final velocity of a ball rolling while slipping.

[brochesspro]

Homework Statement

A solid sphere rolling on a rough horizontal surface with a linear speed $v_0$ collides elastically with a fixed, smooth, vertical wall. Find the speed of the sphere after it has started pure rolling in the backward direction.

Relevant Equations

Conservation of angular momentum.
The moment of inertia of a solid sphere of mass $m$ and radius $R$ is $\frac 2 5mR^2$.

Here is the problem statement along with the figure.

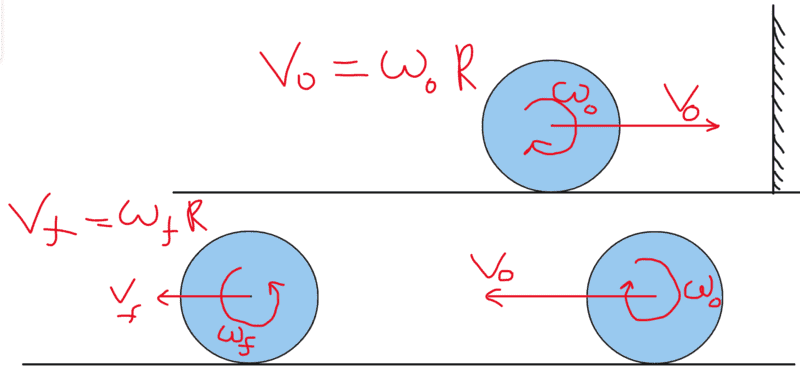
Here, I take the right-ward and anti-clockwise directions to be positive.
After the ball collides with the wall, its angular velocity remains the same and its velocity changes direction while remaining the same in magnitude.
Using the conservation of angular momentum about the bottom-most point, I get:
$-mv_0R -\frac 2 5mR^2\omega_0 = -mv_fR + \frac 2 5 mR^2\omega_f$
$\Rightarrow -mv_0R -\frac 2 5mv_0R = -mv_fR + \frac 2 5 mv_fR$
since $v_0 = R\omega_0$ and $v_f = R\omega_f$
$\Rightarrow -\frac 7 5 mv_0R = -\frac 3 5 mv_fR$
$\Rightarrow 7v_0 = 3v_f$
$\Rightarrow v_f = \frac 7 3 v_0$
This is clearly false as the sphere slows down due to friction acting in the positive direction. May I know what exactly I have done wrong?
Thanks.

 

[malawi_glenn]

When can you use conservation of angular momentum? Can you do that when there is slipping?

 

[brochesspro]

When can you use conservation of angular momentum? Can you do that when there is slipping?

You can use the conservation of angular momentum about a point about which the net external torque on the system is zero. Whether slipping occurs or not does not matter, I think.

 

[malawi_glenn]

You can use the conservation of angular momentum about a point about which the net external torque on the system is zero. Whether slipping occurs or not does not matter, I think.

It will be conserved for the entire system yes but not for individual objects. Consider the spinning disc wich you place another disc from above. Torque due to friction will be same but opposite in direction on those two discs, leding to zero net external torque on the system of two discs. But each individual disc will have its angular momentum altered

 

[brochesspro]

It will be conserved for the entire system yes but not for individual objects. Consider the spinning disc wich you place another disc from above. Torque due to friction will be same but opposite in direction on those two discs, leding to zero net external torque on the system of two discs. But each individual disc will have its angular momentum altered

What does this situation have to do with mine? And the system is taken as the rolling sphere, so I do not think it makes a difference.

 

[malawi_glenn]

What does this situation have to do with mine?

It seems to me that you use that angular momentum of that disc is conserved.

 

[brochesspro]

It seems to me that you use that angular momentum of that disc is conserved.

Yes, you are right.

 

[malawi_glenn]

Yes, you are right.

I meant sphere, not disc...

Well its not conserved because spehere is not the entire system here.

 

[brochesspro]

I meant sphere, not disc...

Well its not conserved because spehere is not the entire system here.

What do you mean? And is the system not up to the solver to choose?

 

[malawi_glenn]

What do you mean? And is the system not up to the solver to choose?

You can choose system yes but if your system is the sphere then you have a non zero external torque due to sliding and friction... simple as that

 

[brochesspro]

You can choose system yes but if your system is the sphere then you have a non zero external torque due to sliding and friction... simple as that

How is the net external torque non-zero about the bottom-most point? All three forces on the sphere, i.e. its weight and the contact force(comprising of the frictional force and the normal reaction from the floor) from the floor pass through the bottom-most point of the sphere, which is also its point of contact with the ground.

 

[brochesspro]

To be honest, I think there is a problem with the sign convention I choose, it is just a feeling though.

 

[malawi_glenn]

To be honest, I think there is a problem with the sign convention I choose, it is just a feeling though.

should be this I think
$-mv_0R +\frac 2 5mR^2\omega_0 = -mv_fR - \frac 2 5 mR^2\omega_f$
i.e. change signs of omega

 

[brochesspro]

should be this I think
$-mv_0R +\frac 2 5mR^2\omega_0 = -mv_fR - \frac 2 5 mR^2\omega_f$
i.e. change signs of omega

However, I chose the anticlockwise direction to be the positive direction, so the signs should stay the same according to me.

 

[malawi_glenn]

if v is positive to the right, then clockwise should be positive angular direction. As in the case when the sphere is approaching the wall.

 

[brochesspro]

if v is positive to the right, then clockwise should be positive angular direction. As in the case when the sphere is approaching the wall.

Why so? Is the sign convention not for the solver to choose?

 

[haruspex]

Here, I take the right-ward and anti-clockwise directions to be positive.

$-mv_0R -\frac 2 5mR^2\omega_0 = -mv_fR + \frac 2 5 mR^2\omega_f$

Why $-mv_0R$? I thought you were taking anticlockwise rotation as positive. After the collision, the velocity is $-v_0$.

 

[brochesspro]

Why $-mv_0R$? I thought you were taking anticlockwise rotation as positive. After the collision, the velocity is $-v_0$.

I see what mistake I did, thanks. I have corrected my mistake. I have gotten the correct answer of $v_f = -\frac 3 7v_0$. Thanks for your help.

 

[malawi_glenn]

Why so? Is the sign convention not for the solver to choose?

Then you need to adjust the condition for pure rolling too.

 

[jbriggs444]

You can choose system yes but if your system is the sphere then you have a non zero external torque due to sliding and friction... simple as that

We are evaluating angular momentum and torque about the lab bench -- the point O. There is no torque about this point because the only relevant force (friction) has a line of action that passes through point O.

So angular momentum is conserved during the post-collision spin-up. Angular momentum about this axis is not conserved during the collision.

There is an angular momentum balance that can be written down. However, it is not the one you are thinking of.

 

[malawi_glenn]

We are evaluating angular momentum and torque about the lab bench -- the point O. There is no torque about this point because the only relevant force (friction) has a line of action that passes through point O.

So angular momentum is conserved during the post-collision spin-up. Angular momentum about this axis is not conserved during the collision.

There is an angular momentum balance that can be written down. However, it is not the one you are thinking of.

yeah I could not see the figure properly I thought O was the point of impact on the wall :)

 

[erobz]

Trying to wrap my head around this. Is the entire initial rotational energy $\frac{1}{2}I \omega_o^2$ required to be converted to heat?

On a frictionless table I would expect it bounces off the wall at $-v_o$, but maintains its initial rotational kinetic energy throughout the duration of motion.

So I'm thinking if its going to change its direction of rotation on a rough surface, its angular velocity must pass through zero (at the end of its slipping motion phase) before pure rolling may resume?

EDIT:

I see that what I'm thinking can't be correct. The change in energy is $\frac{4}{7}mv_o^2$, and the initial rotational KE is $\frac{1}{5}mv_o^2$.

So its losing all its initial rotational KE and some translational KE on top of that in the process between the final state and the collision with the wall. That seems to make sense.

 

[jbriggs444]

So I'm thinking if its going to change its direction of rotation on a rough surface, its angular velocity must pass through zero (at the end of its slipping motion phase) before pure rolling may resume?

Right. That is the picture in my mind's eye.

We have an elastic collision. But the ball is still spinning in its original direction. This is wrong for its new velocity. So it continues to spin one way while moving the other. It spins down through zero angular velocity (we assume!) and then picks up angular velocity in its new direction of forward motion until, eventually, the spin rate and the movement rate match up for rolling without slipping.

It may be worth checking the results of our algebra to make sure that spinning actually stops before rolling without slipping is achieved. Having practiced rolling a hula-hoop with backspin on it for fun, I know for a fact that such will not be achieved for all combinations of forward velocity, backward spin and moment of inertia.

 

[erobz]

It may be worth checking the results of our algebra to make sure that spinning actually stops before rolling without slipping is achieved. Having practiced rolling a hula-hoop with backspin on it for fun, I know for a fact that such will not be achieved for all combinations of forward velocity, backward spin and moment of inertia.

Yeah, I figure I'd might as well just check after posting that. From what I'm getting it loses all its rotational KE and a portion of its translational KE as well in the process between the wall and its final state.

 

[jbriggs444]

Yeah, I figure I'd might as well just check after posting that. From what I'm getting it loses all its rotational KE and a portion of its translational KE as well.

I've not done the calculation. My intuition is that for a solid sphere, it will pick some rotational KE back up. It is certain that the final translational KE and final rotational KE will be in direct proportion. The constant of proportionality will depend on the moment of inertia of the shape.

 

[haruspex]

It may be worth checking the results of our algebra to make sure that spinning actually stops before rolling without slipping is achieved.

Do you not trust the algebra in post #1, as corrected in post #18? It should produce the right sign for the velocity. The same equations of motion apply throughout, even if the velocity is instantaneously zero at some point.

 

[jbriggs444]

Do you not trust the algebra in post #1, as corrected in post #18? It should produce the right sign for the velocity. The same equations of motion apply throughout, even if the velocity is instantaneously zero at some point.

I had not reviewed the algebra in post #1 or #18. The result in #18 after correcting for the sign error seems plausible. However, I want to attack the problem in a slightly different way. Rather than verifying algebra, I want to verify an intuition. Always try to test with a different approach from the one used to generate the result.

Pre impact we have angular momentum of $v_0 R$ from the linear motion of the ball and $\frac{2}{5}v_0 R$ from its rotation. Total $\frac{7}{5}v_0 R$. Clockwise. That part of the algebra was solid.

Post impact the linear motion is reversed but the rotational motion is not. So we should have a total of $\frac{3}{5}v_0 R$. We are subtracting now rather than adding. Clearly the linear contribution is dominating. So the total should be counter-clockwise.

Final angular momentum is $\frac{3}{5}v_0 R$ counterclockwise. Initial angular momentum was $\frac{7}{5}v_0 R$ clockwise. Angular momentum (when rolling without slipping) is proportional to linear velocity. So the result that $v_f = - \frac{3}{7} v_0$ is upheld.

Since the final velocity is in the direction away from the barrier, we are not facing the case where the backspin dominates and a second collision with the barrier ensues.

If I am not mistaken, one would need a thin hoop for backspin to cancel with linear momentum. One would need a rather more exotic mass distribution to go past $I=mR^2$ and get backspin to dominate.

 

[erobz]

I still don't understand how the sign convention works...

If I choose $\rightarrow^+$, $\circlearrowright^+$, I keep getting:

$$ mRv_o + \frac{2}{5}mRv_o = -mRv_f -\frac{2}{5}mR v_f$$

Obviously that's not the result...but I can't see why for some reason?

 

[haruspex]

I still don't understand how the sign convention works...

If I choose $\rightarrow^+$, $\circlearrowright^+$, I keep getting:

$$ mRv_o + \frac{2}{5}mRv_o = -mRv_f -\frac{2}{5}mR v_f$$

Obviously that's not the result...but I can't see why for some reason?

You are making the same mistake as in post #1. The velocity after the collision is $-v_0$.
You seem to be taking $v_f$ as positive left, which is a bit confusing.

 

[haruspex]

One would need a rather more exotic mass distribution to go past I=mR2 and get backspin to dominate.

E.g. a yoyo structure, where the narrow radius in the middle is what contacts the frictional surface.