The Fundamental Theorem of Algebra

Click For Summary
SUMMARY

The discussion centers on the Fundamental Theorem of Algebra, specifically addressing the notation "a^n ≠ 0" in the context of polynomial equations. Participants clarify that this notation refers to the condition that the leading coefficient of a polynomial must be non-zero, ensuring it is a genuine nth-degree polynomial. The conversation highlights the importance of understanding polynomial structure in complex analysis.

PREREQUISITES
  • Understanding of polynomial equations and their degrees
  • Familiarity with complex numbers and their properties
  • Basic knowledge of mathematical notation and terminology
  • Experience with algebraic concepts
NEXT STEPS
  • Study the Fundamental Theorem of Algebra in detail
  • Explore polynomial factorization techniques
  • Learn about complex analysis and its applications
  • Review algebraic structures and their properties
USEFUL FOR

Mathematics students, educators, and anyone interested in algebraic theory and complex analysis will benefit from this discussion.

SprucerMoose
Messages
62
Reaction score
0
Hi all,
I'm currently flicking through and old textbook and came across the following.

"Every polynomial of the form
P(z)%20=%20a_{0}x^{n}%20+%20a_{1}x^{n-1}%20+%20a_{2}x^{n-2}%20+%20...%20+%20a_{n-1}x%20+%20a_{n}.gif
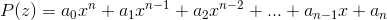, where
gif.latex?a^{n}\neq0.gif
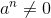has n linear factors over C...". What does it mean by [URL]http://latex.codecogs.com/gif.latex?a^{n}\neq0?[/URL] Is this referring to some kind of complex index? This is all that is written and nothing precedes it. I just don't quite understand the
gif.latex?a^{n}\neq0.gif
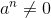.Edit: Latex kind of fixed
 
Last edited by a moderator:
Mathematics news on Phys.org
Hi SprucerMoose! :smile:

(try using the X2 and X2 icons just above the Reply box :wink:)

it must be a misprint for "where a0 ≠ 0" …

in other words, where it's a genuine nth-degree polynomial :smile:
 
Ah, I see. Thank you very much.Testing...

a2 + a0 + a1

Edit: It works!
 
SprucerMoose said:
Testing...

a2 + a0 + a1

Edit: It works!

Now you really are sprucer! :biggrin:
 
SprucerMoose said:
Ah, I see. Thank you very much.


Testing...

a2 + a0 + a1

Edit: It works!
Do you mean a2 + a0 + a1?
 
Mark44 said:
Do you mean a2 + a0 + a1?

Do you mean a2 + a0 + a1?
 
Top that! :smile:

SprucerMoose wins! :biggrin:​
 

Similar threads

Undergrad Question about the Fundamental Theorem of Algebra
  • · Replies 14 ·
Replies
14
Views
3K
High School Extending the Fundamental Theorem of Arithmetic to the rationals
  • · Replies 35 ·
2
Replies
35
Views
5K
Undergrad Fundamental theorem of algebra and factoring?
  • · Replies 6 ·
Replies
6
Views
2K
Graduate So-called Fundamental Theorem of Algebra
  • · Replies 1 ·
Replies
1
Views
2K
High School Confusion about The Conjugate Roots Theorem
  • · Replies 8 ·
Replies
8
Views
2K
Undergrad Why the Fundamental Theorem of Algebra & Calculus are Called "Fundamental
  • · Replies 3 ·
Replies
3
Views
4K
Undergrad If pair of polynomials have Greatest Common Factor as 1 ....
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Prove an nth-degree polynomial has exactly n roots
  • · Replies 3 ·
Replies
3
Views
7K
Undergrad The Fundamental Theorem of Algebra
  • · Replies 6 ·
Replies
6
Views
3K
Python Python’s Sympy Module and the Cayley-Hamilton Theorem
  • · Replies 1 ·
Replies
1
Views
2K