The missing factor of 2π in reciprocal lattice calculations

[Wrichik Basu]

$\require{physics}$ Recently, I wet my feet in X-ray diffraction a bit more than what is usually covered in standard solid state physics textbooks at the undergrad level, like Kittel. Two good books that I chanced upon included Christopher Hammond, The Basics of Crystallography and Diffraction and B. D. Cullity and S. R. Stock, Elements of X-Ray Diffraction. I will, however, stick to Kittel and Hammond in this thread.

In Kittel, the relation between the translation vector in real (or direct) space, $\va{R},$ and that in the reciprocal space, $\va{G},$ is given by $$\begin{align}
&\phantom{implies} \mathrm{e}^{i \va{G} \vdot \va{R}} = 1 \\
&\implies \va{G} \vdot \va{R} = 2\pi m; \quad m \in \mathbb{Z}.
\end{align}$$
If I write $\va{G} = h \va{g}_1 + k \va{g}_2 + \ell \va{g}_3$ and $\va{R} = \sum\limits_{i=1}^3 n_i \va{a}_i$ with $n_i \in \mathbb{Z},$ we can write $$\begin{equation}
\va{g}_i \vdot \va{a}_j = 2 \pi \delta_{ij} \label{eq:g_dot_a_kittel}
\end{equation}$$according to Kittel Chapter 2, and I can follow the reasoning fine.

In Hammond, however, this relation is written as $$\begin{equation}
\va{g}_i \vdot \va{a}_j = \delta_{ij},
\end{equation}$$omitting the $2\pi.$

In all derivations throughout Chapter 8 in Hammond, this relation is used. Thus, $\abs{ \va{G}_{hk\ell} }$ becomes $1/d_{hk\ell},$ the radius of Ewald's sphere becomes $1/\lambda,$ and the vector form of Bragg's law, $$\begin{equation}
\dfrac{\vu{s} - \vu{s}_0}{\lambda} = \va{G}_{hk\ell}, \label{eq:bragg_law_vector}
\end{equation}$$when combined with the first Laue equation, becomes $$\begin{align}
&\phantom{\implies} \va{a} \vdot \qty( \vu{s} - \vu{s}_0 ) = n_x \lambda \nonumber \\
&\implies \va{a} \vdot \va{G}_{hk\ell} \cdot \lambda = n_x \lambda \nonumber \\
&\implies h = n_x,
\end{align}$$with a factor of $2\pi$ missing everywhere.

Things aggravate when Hammond derives the equation for the structure factor in Chapter 9, as follows:

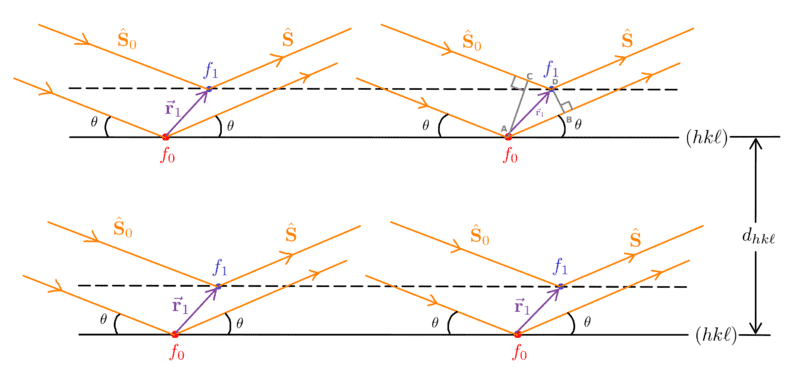
The position vector $\va{r}_1$ is written as$$\begin{equation}
\va{r}_1 = \sum_{i=1}^3 x_i \va{a}_i
\end{equation}$$where $\va{a}_i$ are the lattice basis vectors, and $x_i$ are \textit{fractions} of the cell edge lengths.

The path difference,$$\begin{align}
\mathrm{P.D.} &= \mathrm{AB} - \mathrm{CD} \nonumber \\
&= \va{r}_1 \vdot \vu{S} - \va{r}_1 \vdot \vu{S}_0 \nonumber \\
&= \va{r}_1 \vdot ( \vu{S} - \vu{S}_0 ).
\end{align}$$
$\because$ Bragg's Law is satisfied, we can write using $\text{eqn.}~\eqref{eq:bragg_law_vector}$,$$\begin{align}
&\phantom{\implies} ( \vu{S} - \vu{S}_0 ) = \lambda \va{G}_{hk\ell} \nonumber\\
&\phantom{ \implies ( \vu{S} - \vu{S}_0 ) } = \lambda \qty( h \va{g}_1 + k \va{g}_2 + \ell \va{g}_3 ).\\
&\implies \mathrm{P.D.} = \lambda \qty( x_1 \va{a}_1 + x_2 \va{a}_2 + x_3 \va{a}_3 ) \vdot \qty( h \va{g}_1 + k \va{g}_2 + \ell \va{g}_3 ) \nonumber \\
&\implies \mathrm{P.D.} = \lambda \qty( h x_1 + k x_2 + \ell x_3 ). \label{eq:path_difference}
\end{align}$$where we have used $\va{g}_i \vdot \va{a}_j = \delta_{ij}$ to arrive at the last step.

The phase angle is given by$$\begin{align}
\phi &= \dfrac{2\pi}{\lambda} \mathrm{P.D.} \nonumber \\
&= 2 \pi \lambda \qty( h x_1 + k x_2 + \ell x_3 ).
\end{align}$$

Adding the scattering amplitudes $f$ with their respective phase angles $\phi$ in the complex plane,$$\begin{equation}
\boxed{F_{hk\ell} = \sum_{n = 1}^N f_n ~ \exp \qty[ 2\pi i \qty( h x_n + k y_n + \ell z_n ) ].}
\end{equation}$$

Note that if I simply put the factor of $2\pi$ in $\text{eqn.}~\eqref{eq:path_difference},$ the expression for the phase angle will have a factor of $4\pi^2,$ so will the expression for structure factor. Now, Wikipedia states that this expression for the structure factor is correct, so I just can't put in the $2\pi$ factor.

Can anyone please explain where the $2\pi$ factor is being normalized? And how do I derive the structure factor equation if I want to stick to the expression used in Kittel, i.e. $\text{eqn.}~\eqref{eq:g_dot_a_kittel}?$

Interestingly, I just noticed that @ergospherical has also skipped the $2\pi$ factor in one of my previous thread on the Ewald sphere.

 

[Haborix]

Does the equivalent of Eq. 1 in Hammond have a $2\pi$ in the exponent?

 

[Wrichik Basu]

Does the equivalent of Eq. 1 in Hammond have a $2\pi$ in the exponent?

As far as I can see, Hammond has not written the equivalent of Eq. 1 anywhere, at least from Chapters 6 to 9. Chapter 6 deals with the reciprocal lattice, and there, he directly writes $\va{g}_i \vdot \va{a}_j = \delta_{ij}$ owing to the fact that $\va{g}_1$ is $\perp$ to both $\va{a}_2$ and $\va{a}_3,$ and so on. I didn't read through chapters 1-6 because I already studied them from Kittel.

 

[Haborix]

I don't have any of the textbooks at hand, but I would guess the two $\vec{\mathbf{g}}$ are related by a factor of $2\pi$.

 

[sophiecentaur]

I don't have any of the textbooks at hand, but I would guess the two $\vec{\mathbf{g}}$ are related by a factor of $2\pi$.

It's the same as when choosing between f (frequency) and ω (angular frequency). Neither is 'correct' but the one which avoids a page full of π's is easier to write and interpret.