The physics meaning of the light cones tipping over

[extrads]

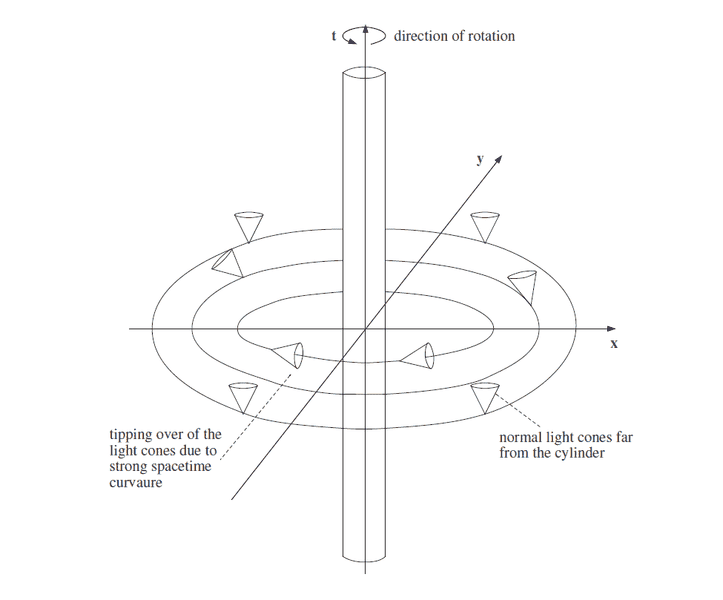
There is a connection between the origin and the points in the light cone.That is to say,there is a casual relationship between them.I think normal light cone means light which travels to the right side and to the left side have the same speed.Then in certain spacetime,eg. at the point of strong spacetime curvature in the picture,the light cones tip over to the right.What does it mean? the light travels faster to the right than to the left? And if the x-axis is the axis of symmetry of the light cone(as the picture shows),it means the origin has connection with the past events?Is it related to CTC(closed timelike curves)?Further more,is there a relationship between the direction of rotation(as the picture shows) and the the direction of tipping over of the light cones?

 

[tiny-tim]

hi extrads!

… in certain spacetime,eg. at the point of strong spacetime curvature in the picture,the light cones tip over to the right.What does it mean? the light travels faster to the right than to the left?

in the ergosphere of a rotating black hole (a narrow region just outside the event horizon), nothing can stand still, it has to rotate in the same direction as the black hole itself

the closer it is to the event horizon, the faster it has to rotate

in its own frame of reference, light behaves normally: it goes left and right at equal speeds

your diagram shows it as viewed by an observer outside the ergosphere: that is not an inertial observer for a point inside

that's all there is to it … you're using a non-inertial frame, so obviously the inertial-frame-physics doesn't apply ​

(i think it's the same on earth: in the laboratory frame … which is non-inertial … light is measured as moving slightly faster down than up: it only has the same speed in opposite directions in inertial, ie free-falling, frames)

 

[WannabeNewton]

You're looking at this incorrectly. The local light cone structure of a curved space-time is identical to the trivial light cone structure of flat space-time. At each event in space-time we isometrically map the trivial light cone with vertex at an arbitrary origin of flat space-time into the tangent space at that event (with vertex at the neutral element) in the curved space-time. Hence the light cone structure is preserved when mapping from flat space-time to the tangent space; we can always pick an orthonormal basis for the tangent space and write down the equation of the light cone in the tangent space as $(v^0)^2 - (v^1)^2 - (v^2)^2 - (v^3)^2 = 0$ where $v^{\mu}$ is a vector in the tangent space (evidently a null vector).

The difference between causal structure of a curved space-time and flat space-time occurs at the global level i.e. the way in which the local light cones vary from event to event. In other words its not the local light cones that are different (they aren't-as already stated the local light cone structure at any given event is just that of flat space-time) but rather the smooth variation in the local light cones as we go from event to event in space-time. So, to reiterate, locally you cannot distinguish a light cone from a light cone in flat space-time with vertex at an arbitrary origin; the distinguishing features of causal structure only come about globally. This is a theorem that's proven in many GR textbooks.

The non-trivial global features come about because of non-trivial topology. A simple but extremely common example is as follows. Take two-dimensional flat space-time and identity two lines of constant time in order to get a cylinder with topology $S^1 \times \mathbb{R}$ where $S^1$ corresponds to the "time dimension". As you can easily picture, the light cones at each point on the cylinder look the exact same as light cones in flat space-time but because of the relatively non-trivial topology we're considering here the light cones start tipping as we move around the cylinder; in fact we get closed time-like curves. The point is when we consider curved space-times $(M,g_{\mu\nu})$, $M$ will necessarily have a non-trivial topology giving rise to non-trivial global causal structure.

P.S. when I say "non-trivial" topology I mean one that isn't equivalent to the canonical topology of flat space-time and not in the sense of fundamental groups.

 

[bcrowell]

The tipping of the light cones isn't something that exists in the Minkowski coordinates (t,x,y,z) of any observer. In any such coordinates, the right and left sides of the light cone have the usual slope \pm1 (in units where c=1), because the speed of light is the same for all observers. However, if you take some coordinate system such as the Schwarzschild coordinates for a Schwarzschild black hole, the light cone appears tipped on a graph using those coordinates. It's the same idea as the distortions on a flat map of the earth.

 

[bcrowell]

The non-trivial global features come about because of non-trivial topology.

The issue isn't topology, it's curvature. For example, the Schwarzschild spacetime has the same topology as Minkowski space, but its light cones are tipped.

 

[WannabeNewton]

The issue isn't topology, it's curvature.

The cylinder example is locally isometric to flat space-time.

For example, the Schwarzschild spacetime has the same topology as Minkowski space, but its light cones are tipped.

Schwarzschild has the product topology $\mathbb{R}\times (p, \infty) \times S^2$ where $p > 0$. How is this the same as the Euclidean topology $\mathbb{R}^4$?

 

[Bill_K]

It's not topology or curvature, it's coordinates. Light cones are not tipped in the Schwarzschild spacetime if you use Kruskal coordinates.

 

[JesseM]

It's not topology or curvature, it's coordinates. Light cones are not tipped in the Schwarzschild spacetime if you use Kruskal coordinates.

Based on the diagram, I think the original poster wasn't talking about the tipping of light cones in a coordinate system in a black hole spacetime, but rather in the spacetime of a Tipler Cylinder, a spinning rod of infinite length that would allow for closed timelike curves in the vicinity of the rod.

 

[bcrowell]

It's not topology or curvature, it's coordinates. Light cones are not tipped in the Schwarzschild spacetime if you use Kruskal coordinates.

Well, it's both curvature and coordinates. If there's no curvature, then coordinates exist in which the light cones don't tip. If there's curvature, then no such coordinates exist.

 

[JesseM]

Well, it's both curvature and coordinates. If there's no curvature, then coordinates exist in which the light cones don't tip. If there's curvature, then no such coordinates exist.

Are you saying there's no curvature in the spacetime describing an eternal Schwarzschild black hole? As Bill_K said, if you describe that spacetime geometry using Kruskal-Szekeres coordinates, the light cones don't tip. And by "no curvature" do you mean that all the components of one or more curvature tensors go to zero, or something else?

 

[PAllen]

Rather than focusing on tipping of light cones (which, locally, is a non-sequiter), one can focus on global geometry.

Outside the horizon, you cannot make a spacelike slice that has continuous family 2-spheres of constant area. You can make make 2-spaceX1time slice of this nature. Inside the horizon, you can make a spacelike slice of this kind. To my mind, this is an invariant analog of what 'light cone tipping' is getting at. A type of hypersurface that must be 2X1 outside the horizon can be purely spatial inside the horizon.

 

[WannabeNewton]

It's not topology or curvature, it's coordinates. Light cones are not tipped in the Schwarzschild spacetime if you use Kruskal coordinates.

I see your point and I agree with you about the coordinate dependent nature of the "tipping of light cones". It is however a very well known fact that global causal structure and topology are strongly related in "well-behaved" cases so I should have referred specifically to global causal structure and left out the "tipping of light cones".

 

[PAllen]

Rather than focusing on tipping of light cones (which, locally, is a non-sequiter), one can focus on global geometry.

Outside the horizon, you cannot make a spacelike slice that has continuous family 2-spheres of constant area. You can make make 2-spaceX1time slice of this nature. Inside the horizon, you can make a spacelike slice of this kind. To my mind, this is an invariant analog of what 'light cone tipping' is getting at. A type of hypersurface that must be 2X1 outside the horizon can be purely spatial inside the horizon.

Yet another way to put this is, instead of dubious light cones tipping, talk about a killing vector field 'tipping' - changing nature. Outside the horizon, the extra (besides spherical symmetry) killing vector describing the 'direction' in which the geometry doesn't change is timelike. Inside the horizon, the geometry is not stationary; instead there is an extra spatial direction in which the geometry doesn't change - the axial direction of the 3-cylinders I described. The change in 'direction' of the extra killing vector field is not a coordinate artifact.

 

[bcrowell]

Are you saying there's no curvature in the spacetime describing an eternal Schwarzschild black hole? As Bill_K said, if you describe that spacetime geometry using Kruskal-Szekeres coordinates, the light cones don't tip. And by "no curvature" do you mean that all the components of one or more curvature tensors go to zero, or something else?

Hmm...good point. I guess any time you can draw a conformal diagram of a spacetime, you're picking coordinates in which the light cones don't tip.