Light cone shape while speeding up

[The Count]

Hello

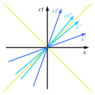
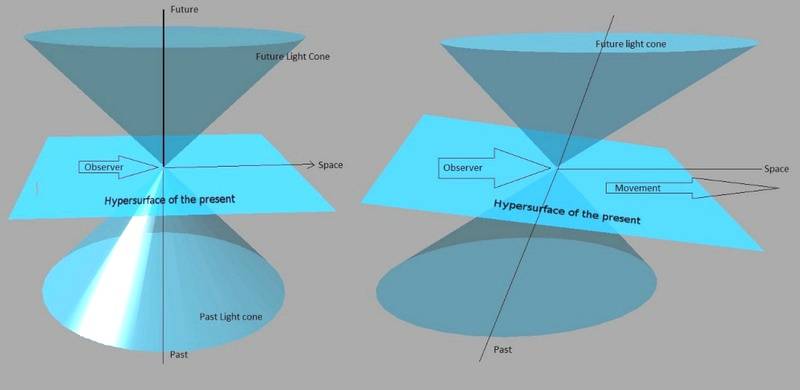
I searched a lot but I am not sure if I understood correctly the change in the shape of light cone while speeding up. I am aware that the x and ct axis are getting closer to each other like scissors while you speed up as the graph below shows, both symmetricaly approaching the ct=x or v=c line.

But I am not sure if there is a corresponding graph that shows the shape of the light cone.
I have found the following cases.
1. Stays the same, keeping its shape, its angle (45^o), its circularity.

2. Its direction is now parallel to ct' axis, it keeps the circularity, its symmetrical shape is now round ct' axis and not ct, its opening angle closes and equals the angular difference between ct' and ct=x line (light cone boundaries), until it goes zero when v=c. Then the light cone is just a line.

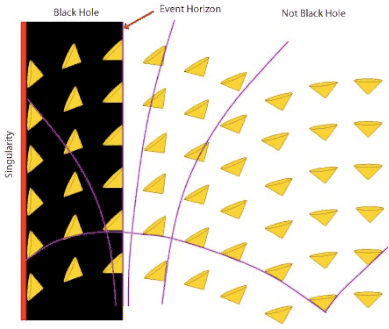
Unfortunately most shapes are from black hole cases, but as I recall gravity is the same as acceleration. Here also rises the question how the light cone also changes in constant speed with no acceleration.

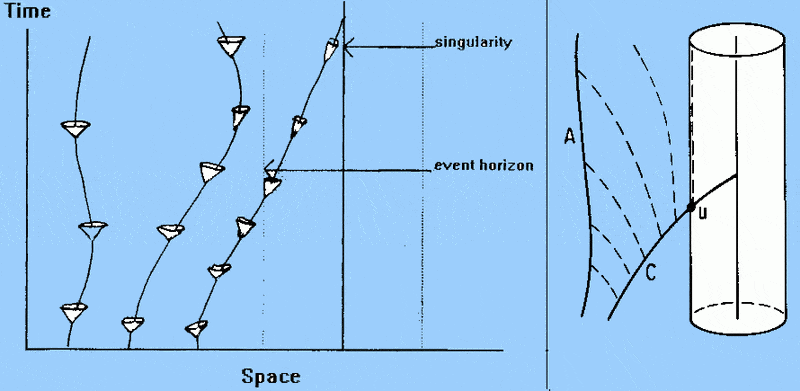3. It keeps its upward direction but it loses its symmetrical shape round ct axis. Maybe the slice of the future that was a circle with center the axis ct, is now an elipse with two centers, ct axis and ct' axis. The rather radical about this light cone is that it overpasses the initial light cone boundaries and goes under the line ct=x (or v=c). This seems to violate GR rules. In this diagram while in the same direction we go below ct=x, in the opposite we keep ct=-x the boundary.

4. It keeps its symmetrical round shape with the same angle but now round ct' axis. Maybe the slice of the future (perpendicular to ct' now) remains a circle but with center the axis ct'. The rather radical also about this light cone is that it overpasses the initial light cone boundaries and goes under the line ct=x (or v=c). This seems to violate GR rules. In this diagram while in the same direction we go below ct=x, in the opposite we don't keep ct=-x as boundary instead we follow the same angle as ct' to old ct.

As I said I am aware that all the above graphs are not exactly the same but with the equivalense of gravity and acceleration and the "hypothetical" invariance of lightcone representation they should in a way (if not exactly) agree in principle.

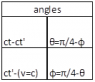
I tried to sum up some details in a table.

I would appreciate a comment (even short) for each case and if possible for both constant speed and acceleration.

Thanks in advance for your time.

 

[PeterDonis]

I have found the following cases.

To the extent that these different "cases" are even valid (see below), they refer to different physical spacetimes, only one of which (the first one) corresponds to the diagram you give of how the ct-x axes change under a Lorentz transformation. That's because if you're doing a Lorentz transformation, you've already assumed that you're working in Minkowski spacetime (the flat spacetime of SR), in which the light cone behavior is as you describe it in case #1. In other spacetimes (such as black hole spacetimes), there is no such thing as a Lorentz transformation covering all of the spacetime, so the ct-x axis diagram you give doesn't even apply.

most shapes are from black hole cases, but as I recall gravity is the same as acceleration

No, it isn't. The correct statement of the equivalence principle is that, locally (the qualifier is key--see below), being at rest inside an accelerating spaceship is the same as being at rest in a gravitational field (provided the acceleration you feel is the same in both cases). But "gravity" is much more than just being at rest in a gravitational field, and the equivalence is only local anyway--it doesn't extend through all of spacetime, so it doesn't help you in trying to understand something global like how the light cones behave.

The reason the light cone behavior, globally, is different in black hole cases is that spacetime is curved, not flat. Also, the light cone behavior you are talking about in the black hole case (as shown in the diagrams you give) is a change in the light cones as you move from one location to another in spacetime. That's not the same as how (if at all) the appearance of the light cones in a spacetime diagram is affected when you do a Lorentz transformation at a particular event, which is what the start of your post is talking about. So you're confusing two different things.

I am aware that all the above graphs are not exactly the same but with the equivalense of gravity and acceleration and the "hypothetical" invariance of lightcone representation they should in a way (if not exactly) agree in principle.

No. You're mixing up different cases. See above.

 

[The Count]

Thanks for the answer.

As I understood the correct answer is 1. This seemed correct to me too but I got confused with all the other graphs.

I would appreciate if you helped me with some questions.

the ct-x axis diagram you give doesn't even apply.

You mean there is no diagram ct-x that applies or the ones that I gave are wrong? Can you give more feedback please?
If the case is that these bend light cones are the ones that other observers are supposed to see when one falls in a black hole and not the "proper" light cone of the one that falls, shouldn't this apply also to the one accelerating?

The reason the light cone behavior, globally, is different in black hole cases is that spacetime is curved, not flat.

Isn't the tilt of ct' and x' axis a curvature in their spacetime? Shouldn't they feel the exact same time dilation and length contraction? Everybody on the accelerating spaceship and respectively from the black holes' gravity should have the same experience, correct?

is a change in the light cones as you move from one location to another in spacetime.

We just have to continuously increase the acceleration to be similar with the fall into the black hole. Isn't this the same?
I believe we can simulate a path of a fall in a black hole with a respectively accelerating pattern. They should both have light cones, shouldn't be the same?

Finally in case 4. the grad of the light cone overpasses 45^o. This is wrong, isn't it? In event horizon it shows to be 90^o and in the center 135^o from initial ct. The correct graph for black holes is case 2. correct?

Thanks again for your time.

 

[PeterDonis]

As I understood the correct answer is 1.

For the case of flat spacetime, yes. But a black hole spacetime is not flat spacetime; that's why the other graphs look different.

You mean there is no diagram ct-x that applies

There are coordinate charts that apply to black holes--the other images you gave are based on different coordinate charts that apply to black holes. But thinking of them as "ct-x" diagrams is probably not a good idea. Some of the charts (such as the first one under your item 2) don't even have timelike coordinates, so there is no analogue to "ct" in them.

Can you give more feedback please?

I already did: I told you that gravity is not the same as acceleration. The analogy you are trying to use to understand the black hole diagrams is wrong and will not help you.

Isn't the tilt of ct' and x' axis a curvature in their spacetime?

As I said above, the tilt in the other diagrams is not a tilt in the "ct" and "x" axis. Some of the charts being used do not even have timelike coordinates, so there is no "ct", and the "spatial" coordinate is the radial coordinate r, not x, and does not directly measure distance.

It does happen to be the case that the tilting of the light cones in the black hole diagrams is due to spacetime curvature; but that is not always the case. You can find coordinate charts on flat spacetime that make the light cones look tilted.

Shouldn't they feel the exact same time dilation and length contraction?

No. First of all, nobody "feels" time dilation or length contraction; those are things that other people, observing you, might see, but you never see yourself as time dilated or length contracted. Second, "time dilation" and "length contraction" are derived concepts that don't really apply to black holes, at least not the way you are trying to apply them. As I said above, the analogy you are trying to make between gravity and acceleration is wrong.

Everybody on the accelerating spaceship and respectively from the black holes' gravity should have the same experience, correct?

No. People free-falling into the black hole feel zero acceleration. People in the accelerating spaceship do not; they feel nonzero acceleration.

We just have to continuously increase the acceleration to be similar with the fall into the black hole. Isn't this the same?

No.

I believe we can simulate a path of a fall in a black hole with a respectively accelerating pattern.

Your belief is incorrect.

in case 4. the grad of the light cone overpasses 45^o. This is wrong, isn't it?

No.

The correct graph for black holes is case 2. correct?

They are all correct; they are different coordinate charts on the same spacetime.

 

[DrGreg]

@The Count , there's an analogy to be drawn between coordinate charts in GR and cartographic maps of the Earth.

On flat paper, you can draw an accurately-to-scale map of a small area of the Earth's surface (say a one-mile square or 1 km square) in which all distances are to the same uniform scale and all angles on the map are the same as angles on the ground.

But this isn't possible for flat-paper maps covering most or all of the Earth's surface. There will always be some distortion, and either the scale with vary with position, or map-angles aren't the same as angles on the ground, or North isn't vertical on the map, etc, depending on the map projection, i.e. on the choice of coordinates.

For a similar reason you may find that light cones get distorted when drawn on a spacetime diagram (depending on which coordinates you use).

 

[The Count]

Thanks for your answer PeterDonis .

For the case of flat spacetime, yes.

As a conclusion from your words, in flat spacetime no matter the acceleration or speed, and despite the inclination of the two axis (approaching one another) the light cone remains exactly the same. So No3's case graph is completely wrong. The other graphs are for not flat spacetime. Got that.

You can find coordinate charts on flat spacetime that make the light cones look tilted.

Can you please give an example? A link or anything.

But thinking of them as "ct-x" diagrams is probably not a good idea.

Ok, these graphs do not help. Is there any way to compare light cones in flat and non flat spacetime (like angles, tilting etc)? Is it tottaly wrong to try to compare them in ct-x axis? Are there any graphs that could help in this direction? When I asked for more feedback, I meant if there is any helpfull graph or math equation that could help me deepen on light cones in curved spacetime.

People free-falling into the black hole feel zero acceleration. People in the accelerating spaceship do not; they feel nonzero acceleration.

Yes, I agree with "free falling" people. I might used wrong words. Let's assume that we are talking about a light cone of something standing in fixed distance from a massive object (either because of centripetal force, or just standing on it's surface like us on the earth-not possible in a black hole). So in this case they are feeling the same acceleration, with something else that just accelerates accordingly in flat space. Do they have the same lightcones? Are they tilted or in any way different from the flat space lightcone?

Thanks again for your time.

 

[The Count]

@DrGreg
Thanks for your answer too.
If I am not wrong you are talking about non Euclidean geometries. I must admit that I don't have a deep knowledge of the maths that connect Riemannian or Lobachevsky's geometry with lightcones. If you can provide a link, I would appreciate it.

In any case these geometries, as you said, in small scales they tend to be like Euclidean flat spacetime. Even in these special cases, can't we compare lightcones?

 

[PeterDonis]

in flat spacetime no matter the acceleration or speed, and despite the inclination of the two axis (approaching one another) the light cone remains exactly the same.

That's not quite what I said. What I said, combined with what "case 1" in your OP actually refers to, is this: if you use inertial coordinates in flat spacetime, the light cones look exactly the same in all inertial frames; a Lorentz transformation does not change their shape at all.

Can you please give an example?

Sure, just use non-inertial coordinates. For example, Rindler coordinates; see the diagram here:

https://en.wikipedia.org/wiki/Rindler_coordinates#Minkowski_observers

Note that this diagram is not just about the shape of the light cones, but it does show them. Also, the line at the very left of the diagram, which is the Rindler horizon, is also a light cone (it's the light cone of the event in spacetime that would be the origin of an inertial chart), and it's a vertical line!

Is there any way to compare light cones in flat and non flat spacetime (like angles, tilting etc)?

First you need to think about what, if anything, such a comparison would even mean. What exactly are you trying to compare? And why? Different spacetimes are physically different, so any scheme for "comparing" them has to be carefully defined.

Let's assume that we are talking about a light cone of something standing in fixed distance from a massive object (either because of centripetal force, or just standing on it's surface like us on the earth-not possible in a black hole). So in this case they are feeling the same acceleration, with something else that just accelerates accordingly in flat space. Do they have the same lightcones? Are they tilted or in any way different from the flat space lightcone?

Again, it's not clear what, if anything, such a comparison wouold even mean. The equivalence principle can help some, but only locally, and what it says locally isn't very helpful: locally, you can't tell the difference between a small patch of flat spacetime and a small patch of a curved spacetime, so locally, the light cones seen by the two accelerated observers in question (one "hovering" at a fixed altitude above a black hole, the other accelerating in flat spacetime) are the same. But I don't think that really satisfies you, does it?

The problem is that, as soon as you go beyond a small local patch of spacetime, the two spacetimes are physically different, so it's not even clear how to compare them, or what such a comparison is telling you, physically. What, exactly, do you want to compare? Comparing the "shapes" or the tilting of the light cones isn't really helpful in itself because, as I've said, that depends on the coordinates you choose. So to know how to even approach the question, I think you need to think about why you want to know.

 

[The Count]

Thanks again for your time.

a Lorentz transformation does not change their shape at all.

So if I understood correctly no matter the tilt of the two axis (x,ct) while in high speed (but no acceleration) the lightcone does not change at all it's shape. Isn't the speed determined by the angle to the ct axis? When the ct axis tilts towards the +x section of x axis, then it seems that to get close to the lightcone line of the -x section, the angle is going to be more than 45^o (from the tilted ct axis). This means that it passes over the limit of c, or do the maths change?

But when we have acceleration the light cone changes! The question is how it is changed? It tilts until it "falls" on the +x section of x-axis (case 4), it closes and tilts at the same time until it ends up in a line (case 2), or it tilts and inflates at the same time (case 3). What I am looking for is a diagram (like the first graph) that shows the change of the lightcone when in acceleration. I have not found it no matter how much I searched.

Shouldn't the lightcones of non flat space (that simulates acceleration at least locally) help us in that? If not how can we make such a graph? Shouldn't the same graph be the same for the two observers? The first one accelerating and the second being in the gravitational field of a massive object.

Rindler coordinates; see the diagram here:

Thanks for the example. I have to say that I have to study it carefully, because I have not understood that the vertical line on the left is a light cone too.

 

[Dale]

But when we have acceleration the light cone changes!

I would not say that the light cone changes. I would say that the coordinates change. However, it is correct that the coordinate expression for the light cone is different in non inertial coordinates than in inertial coordinates.

 

[PeterDonis]

Isn't the speed determined by the angle to the ct axis?

Yes. And as that angle approaches 45 degrees, the speed approaches the speed of light. The angle can never reach or cross 45 degrees (i.e., it can never reach or cross the light cone), because nothing material can move at or faster than the speed of light.

(Note that all of this assumes you are using inertial coordinates in flat spacetime. See further comments below.)

when we have acceleration the light cone changes!

No, it doesn't. You can't change the geometry of spacetime by changing your state of motion. The light cones are part of the geometry of spacetime. (Note that this is true not just for accelerated motion in flat spacetime, but for any kind of motion in curved spacetime, i.e., when gravity is present. See further comments below.)

What does change if you use non-inertial coordinates, as Dale says, is how the coordinates describe the light cone. But that's because you changed coordinates, not because anything about the light cones changed.

Similarly, in curved spacetime, there are various coordinates you can choose to describe things, and the light cones might look different in different coordinates--the diagrams you draw will show different shapes and tilts for the light cones depending on which coordinates you choose. But that's because you changed coordinates, not because anything about the light cones changed.

Shouldn't the same graph be the same for the two observers? The first one accelerating and the second being in the gravitational field of a massive object.

No, because the light cones are part of the geometry of spacetime, as above, and the geometry of spacetime is different for the two cases (it's flat in the first case and curved in the second).