Math Amateur
Gold Member
MHB
- 3,920
- 48
I am reading John B. Conway's book: A First Course in Analysis and am focused on Chapter 3: Integration ... and in particular I am focused on Section 3.1: The Riemann Integral ...
I need help with an aspect of the proof of Proposition 3.1.4 ...Proposition 3.1.4 and its proof read as follows:
View attachment 9456
View attachment 9457
In the above proof by John Conway we read the following:
" ... ... Since $$\epsilon$$ was arbitrary we have that there can be only one number between L(f, Q) and U(f, Q) for every such refinement. ... ... "My question is as follows:
Can someone please explain what Conway means by saying that there can be only one number between $$L(f, Q)$$ and $$U(f, Q)$$ for every such refinement and, further explain why this is true ... and then, further yet, why exactly this number is $$\int_a^b f $$ ... Help will be appreciated ...
Peter==========================================================================================The above proof refers to Proposition 3.1.2 so I am making available the statement of the proposition ... as follows:View attachment 9458It may help MHB readers to have access to the start of Section 3.1 preliminary to Proposition 3.1.4 ... so I am providing the same ... as follows:View attachment 9459
View attachment 9460
View attachment 9461
Hope that helps ...
Peter
I need help with an aspect of the proof of Proposition 3.1.4 ...Proposition 3.1.4 and its proof read as follows:
View attachment 9456
View attachment 9457
In the above proof by John Conway we read the following:
" ... ... Since $$\epsilon$$ was arbitrary we have that there can be only one number between L(f, Q) and U(f, Q) for every such refinement. ... ... "My question is as follows:
Can someone please explain what Conway means by saying that there can be only one number between $$L(f, Q)$$ and $$U(f, Q)$$ for every such refinement and, further explain why this is true ... and then, further yet, why exactly this number is $$\int_a^b f $$ ... Help will be appreciated ...
Peter==========================================================================================The above proof refers to Proposition 3.1.2 so I am making available the statement of the proposition ... as follows:View attachment 9458It may help MHB readers to have access to the start of Section 3.1 preliminary to Proposition 3.1.4 ... so I am providing the same ... as follows:View attachment 9459
View attachment 9460
View attachment 9461
Hope that helps ...
Peter
Attachments
-
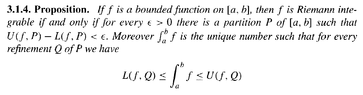 Conway - 1 - Proposition 3.1.4 - PART 1 ... .png8.5 KB · Views: 137
Conway - 1 - Proposition 3.1.4 - PART 1 ... .png8.5 KB · Views: 137 -
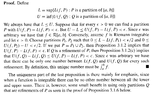 Conway - 2 - Proposition 3.1.4 - PART 2 ... .png26.9 KB · Views: 165
Conway - 2 - Proposition 3.1.4 - PART 2 ... .png26.9 KB · Views: 165 -
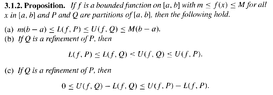 Conway - Proposition 3.1.2 ... .png10.3 KB · Views: 146
Conway - Proposition 3.1.2 ... .png10.3 KB · Views: 146 -
 Conway - 1 - Start of Section 3.1 ... Part 1 .png31.5 KB · Views: 150
Conway - 1 - Start of Section 3.1 ... Part 1 .png31.5 KB · Views: 150 -
 Conway - 2 - Start of Section 3.1 ... Part 2 ... .png60.1 KB · Views: 155
Conway - 2 - Start of Section 3.1 ... Part 2 ... .png60.1 KB · Views: 155 -
 Conway - 3 - Start of Section 3.1 ... Part 3 ... .png42.1 KB · Views: 155
Conway - 3 - Start of Section 3.1 ... Part 3 ... .png42.1 KB · Views: 155
Last edited: