Nano-Passion
- 1,291
- 0
It bugs me how terrible my math classes were in grammar and high school. Many teach the beauty of mathematics at a superficial level. They simply teach you formulas largely through memorization. When it should be taught through assisted self-discovery, showing the bigger picture, etc..
At grammar school the following formula was slapped on the black board: c^2=a^2+b^2
All I saw was a bunch of letters and numbers, no beauty or "coolness factor" was discovered.
If it was taught the reasoning of it all through the teacher slowly showing us why c^2=a^2+b^2 I would have developed a liking towards the concept. Such as with
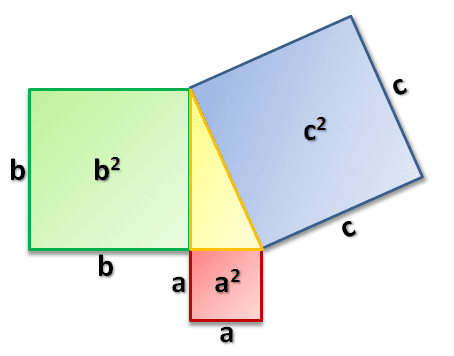
Or through assisted self-discovery was taught the beauty of pi by the following dialogue and reasoning: http://www.worsleyschool.net/science/files/piorigin/piorigin.html
I would have seen more of the beauty of mathematics much earlier.
Seriously now, one of the reason that mathematics isn't one of the more popular fields is because the beauty is much more obscure and only gives itself up under careful scrutiny. It is much easier to develop a connection with other fields (psychology, etc.) because there is an immediate visible connection to the outside world.
Taking mathematics out of context and slapping formulas simply does no merit to the potential beauty that is often hidden by bad teaching.
At grammar school the following formula was slapped on the black board: c^2=a^2+b^2
All I saw was a bunch of letters and numbers, no beauty or "coolness factor" was discovered.
If it was taught the reasoning of it all through the teacher slowly showing us why c^2=a^2+b^2 I would have developed a liking towards the concept. Such as with
Or through assisted self-discovery was taught the beauty of pi by the following dialogue and reasoning: http://www.worsleyschool.net/science/files/piorigin/piorigin.html
I would have seen more of the beauty of mathematics much earlier.
Seriously now, one of the reason that mathematics isn't one of the more popular fields is because the beauty is much more obscure and only gives itself up under careful scrutiny. It is much easier to develop a connection with other fields (psychology, etc.) because there is an immediate visible connection to the outside world.
Taking mathematics out of context and slapping formulas simply does no merit to the potential beauty that is often hidden by bad teaching.