Discussion Overview
The discussion revolves around calculating the required thickness of thermal insulation, particularly in the context of an engine bay with forced air cooling. Participants explore the underlying equations and principles, including heat conduction, convection, and the use of an online calculator for insulation thickness.
Discussion Character
- Exploratory
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
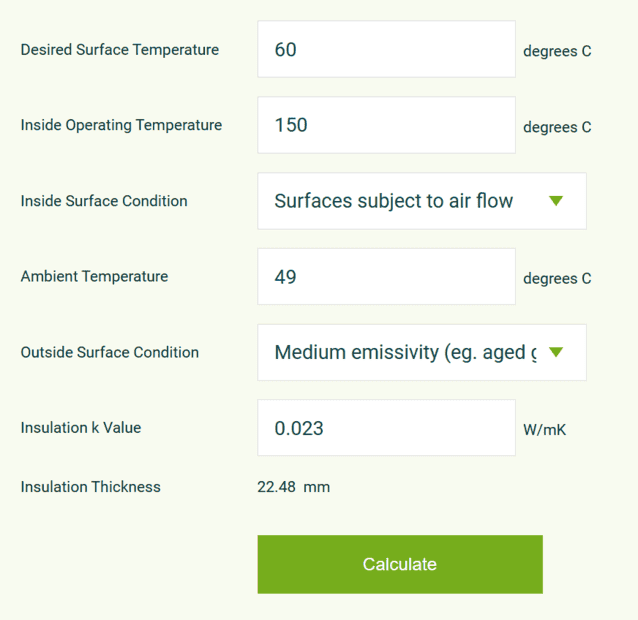
- One participant shares a link to an online calculator for insulation thickness and seeks to understand the equations used in the calculation, suggesting it involves heat conduction and possibly convection and radiation effects.
- Another participant mentions that the calculator employs Fourier's law in one dimension and questions the necessity of reverse-engineering it, suggesting that building a personal calculation might be more beneficial.
- Concerns are raised about whether the calculator accounts for convective heat transfer resistance on both sides of the insulation.
- A participant describes their specific application involving known parameters such as inside and outside air temperatures, material properties, and desired surface temperatures, indicating they are on the right track with their inputs.
- There is a discussion about the heat transfer equation involving the convection heat transfer coefficient and its variability based on experimental conditions, with a reference to typical values for forced convection.
- One participant outlines their approach to calculating insulation thickness using a series of heat transfer equations, but notes discrepancies between their results and those from the calculator, prompting a request for advice on potential errors in their calculations.
- A later reply introduces additional variables and equations to account for temperature differences across various materials, suggesting a more complex model for heat transfer.
Areas of Agreement / Disagreement
Participants express differing views on whether the calculator accounts for convective heat transfer and whether their own calculations align with the results from the calculator. The discussion remains unresolved regarding the accuracy of the calculator and the participants' individual calculations.
Contextual Notes
Participants acknowledge the complexity of heat transfer calculations, including the dependence on various parameters such as the convection heat transfer coefficient, which is experimentally determined and varies with conditions. There are also unresolved mathematical steps in the participants' calculations that may contribute to discrepancies.
 !
!