Homework Help Overview
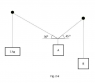
The discussion revolves around a problem involving three masses connected by pulleys, focusing on the relationships between their movements and the geometry of the system. Participants are exploring the mechanics of how one mass's movement affects the others, particularly in terms of displacement and velocity components.
Discussion Character
- Exploratory, Conceptual clarification, Mathematical reasoning, Assumption checking
Approaches and Questions Raised
- Participants discuss the relationship between the movements of the masses, questioning the correctness of initial assumptions about displacement ratios. There are attempts to apply the Pythagorean theorem and virtual work principles to analyze the problem. Some participants express confusion about the geometric relationships and the implications of velocity components.
Discussion Status
The discussion is ongoing, with various participants providing insights and questioning each other's reasoning. Some have offered guidance on visualizing the problem through diagrams and breaking down the components of motion, while others are still grappling with understanding the relationships involved.
Contextual Notes
Participants note the complexity of the problem and the potential for misunderstanding due to the intricate relationships between the masses and the angles involved. There are references to specific angles and components of velocity that are under discussion, indicating that certain assumptions or definitions may need clarification.