Time period of oscillation and gravitation

[Saitama]

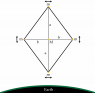
Homework Statement

Homework Equations

The Attempt at a Solution

I really don't know how to start with this problem. The four point masses of mass m oscillate together so I am confused as to how should I begin making the equations. Just a guess, should I write down the expression for potential energy of the system?

Any help is appreciated. Thanks!

 

[mfb]

Just a guess, should I write down the expression for potential energy of the system?

Sure. Add the kinetic energy for the mentioned oscillation afterwards.
This is just a harmonic oscillator (for small excitations).

 

[Saitama]

Sure. Add the kinetic energy for the mentioned oscillation afterwards.
This is just a harmonic oscillator (for small excitations).

This is what I get:
$$E=\frac{2GMm}{a}+\frac{2GMm}{b}+\frac{4Gm^2}{\sqrt{a^2+b^2}}+\frac{Gm^2}{2a}+\frac{Gm^2}{2b}+\frac{G(M+4m)M_e}{R}+2mv^2$$
where $M_e$ is the mass of Earth and $R$ is the radius of orbit.
Is this correct? What should be my next step?

 

[voko]

Do not compute the potential energy of the masses with respect to each other. The satellite is considered rigid, so it is a constant. Compute the the difference in potential energy of the masses with respect to the Earth if the masses are rotated a small angle from the stable position about the central mass. Use the fact that the distances are very much smaller than the radius of the orbit. Then compute the kinetic energy of this small motion.

 

[Saitama]

Do not compute the potential energy of the masses with respect to each other. The satellite is considered rigid, so it is a constant. Compute the the difference in potential energy of the masses with respect to the Earth if the masses are rotated a small angle from the stable position about the central mass. Use the fact that the distances are very much smaller than the radius of the orbit. Then compute the kinetic energy of this small motion.

Please see the attachment.
$$U_i=\frac{GM_em}{R-a}+\frac{GM_em}{R+a}+\frac{2GM_em}{R}+C$$
where C is the potential energy of central mass with respect to Earth and the potential energy of point masses with respect to each other and the central mass.
$$U_f=\frac{GM_em}{R-a\cos\theta}+\frac{GM_em}{R+a\cos\theta}+\frac{GM_em}{R-b\sin\theta}+\frac{GM_em}{R+b\sin\theta}+C$$
I am thinking of using the following approximations:
$$\frac{1}{R-a}=\frac{1}{R}\left(1+\frac{a}{R}\right)$$
and
$$\frac{1}{R-a\cos\theta}=\frac{1}{R}\left(1+\frac{a\cos\theta}{R}\right)$$
Should I replace $\cos\theta$ with $1-\theta^2/2$ for small angle approximation?

How to find the kinetic energy? Do I have to work in the frame of CM? Is it simply $2mv^2$ where v is the velocity of each point mass?

 

[voko]

Your approximation should work, but, personally, I would just find the second derivative with regard to the angle directly, and form $k\theta^2$ as the potential energy due to the small displacement. That should eliminate any concerns about the validity of approximations.

Regarding the kinetic energy, we only care about the motion due to the small displacement, which makes CM the frame of choice.

 

[Saitama]

Your approximation should work, but, personally, I would just find the second derivative with regard to the angle directly, and form $k\theta^2$ as the potential energy due to the small displacement. That should eliminate any concerns about the validity of approximations.

Regarding the kinetic energy, we only care about the motion due to the small displacement, which makes CM the frame of choice.

$$\frac{dU}{d\theta}=GM_em\left(\frac{-a\sin\theta}{(R-a\cos\theta)^2}+\frac{a\sin\theta}{(R+a\cos\theta)^2}+\frac{a\cos\theta}{(R-a\sin\theta)^2}+\frac{-a\cos\theta}{(R+a\sin\theta)^2}\right)$$
Should I simplify this using approximation to find the second derivative or should I go on differentiating this? This seems a bit dirty.

Should I use the approximation:
$$\frac{1}{(R-a\cos\theta)^2}=\frac{1}{R}\left(1+\frac{2a\cos\theta}{R}\right)=\frac{1}{R}\left(1+\frac{2a}{R}-\frac{a\theta^2}{R}\right)$$

 

[voko]

Actually, upon thinking some more, the successive approximations approach results in four terms that cancel one another.

$$ \frac {1} {R - a \cos \theta} + \frac {1} {R + a \cos \theta} \approx \frac 1 R \left( 1 + \frac {a \cos \theta} {R} \right) + \frac 1 R \left( 1 - \frac {a \cos \theta} {R} \right) = \frac 1 R $$

Secondly, the gravitational potential energy must be negative.

 

[voko]

$$\frac{dU}{d\theta}=GM_em\left(\frac{-a\sin\theta}{(R-a\cos\theta)^2}+\frac{a\sin\theta}{(R+a\cos\theta)^2}+\frac{a\cos\theta}{(R-a\sin\theta)^2}+\frac{-a\cos\theta}{(R+a\sin\theta)^2}\right)$$
Should I simplify this using approximation to find the second derivative or should I go on differentiating this? This seems a bit dirty.

The two final terms should have $b$, not $a$. See me previous message as well.

There is no need to be smart here. Just differentiate the four terms treating each as a $f(\theta)g(\theta)$ product; that will give you eight terms, then you let $\theta = 0$ and find $U \approx U_0 + U''(0) \theta^2 / 2$ (throw $U_0$ away then).

 

[Saitama]

There is no need to be smart here. Just differentiate the four terms treating each as a $f(\theta)g(\theta)$ product; that will give you eight terms, then you let $\theta = 0$ and find $U \approx U_0 + U''(0) \theta^2 / 2$ (throw $U_0$ away then).

Ok I found
$$U''(0)=GM_em\left(\frac{-a}{(R-a)^2}+\frac{a}{(R+a)^2}+\frac{4ab}{R^3}\right)$$

How do you get this: $U \approx U_0 + U''(0) \theta^2 / 2$?

 

[voko]

How do you get this: $U \approx U_0 + U''(0) \theta^2 / 2$?

This is Taylor's expansion, which makes use of the fact that $U'(0) = 0$ (why is that so?).

 

[Saitama]

This is Taylor's expansion, which makes use of the fact that $U'(0) = 0$ (why is that so?).

$U'(0)=0$ because at $\theta=0$, the potential energy is minimum according to the given question.

I used the approximations and got
$$U=U_0+\frac{4ab-2a^2}{R^3}\frac{\theta^2}{2}$$
What should I do now?

 

[voko]

Have you found the kinetic energy of the small oscillations? Conservation of total energy should do the rest.

 

[Saitama]

Have you found the kinetic energy of the small oscillations?

Is it $2mv^2$?

 

[voko]

What is $v$ here?

 

[Saitama]

What is $v$ here?

Velocity of point masses.

 

[mfb]

What is the relation between v and θ?
Can you express the kinetic energy with θ? Afterwards, compare it to the potential and kinetic energy of a simple harmonic oscillator.

 

[Saitama]

What is the relation between v and θ?
Can you express the kinetic energy with θ? Afterwards, compare it to the potential and kinetic energy of a simple harmonic oscillator.

From conservation of energy,
$$2mv^2=\frac{2a^2-4ab}{R^3}\frac{\theta^2}{2}$$
$$\Rightarrow v=\frac{\theta}{2R}\sqrt{\frac{2a^2-4ab}{m}}$$
Do you ask me the kinetic energy of a single point mass? I don't really understand where this is heading. :(

 

[voko]

How come the velocities of all the masses are equal?

Re-read the second paragraph in #6.

 

[Saitama]

How come the velocities of all the masses are equal?

Re-read the second paragraph in #6.

Do I have to use conservation of angular momentum?

 

[mfb]

Not all four point-masses will move with the same velocity when they rotate around the central mass, you cannot use a single "v".

What you wrote down is not the conservation of energy. What is the total energy of the system? This will be constant.

Do you ask me the kinetic energy of a single point mass?

Always add the contributions from all four masses, they always move together.

θ describes where in space your objects are. v describes how your objects move. Clearly there is some relation between them, given by the geometry of the setup. You'll need the time-derivative of θ.Angular momentum is not conserved, you don't have a central potential (at least not central with respect to the rotation axis you consider).

 

[Saitama]

Not all four point-masses will move with the same velocity when they rotate around the central mass, you cannot use a single "v".

What you wrote down is not the conservation of energy. What is the total energy of the system? This will be constant.

Always add the contributions from all four masses, they always move together.

θ describes where in space your objects are. v describes how your objects move. Clearly there is some relation between them, given by the geometry of the setup. You'll need the time-derivative of θ.


Angular momentum is not conserved, you don't have a central potential (at least not central with respect to the rotation axis you consider).

I am still confused. Do you mean the velocities of the point masses are of the form: $b\dot{\theta}$ and $a\dot{\theta}$?

 

[haruspex]

Do I have to use conservation of angular momentum?

Consider the moment of inertia of the system and the KE for a rate of rotation.

 

[voko]

Do I have to use conservation of angular momentum?

I am not sure how you got that from #6. What are the velocities in the CM frame?

 

[Saitama]

I am not sure how you got that from #6. What are the velocities in the CM frame?

$a\dot{\theta}$ and $b\dot{\theta}$?

 

[voko]

$a\dot{\theta}$ and $b\dot{\theta}$?

What makes you confused about this?

 

[Saitama]

What makes you confused about this?

So the kinetic energy is
$$ma^2\dot{\theta}^2+mb^2\dot{\theta}^2$$
From conservation of energy
$$U_0=U_0+GM_em\frac{4ab-2a^2}{R^3}\frac{\theta^2}{2}+ma^2\dot{\theta}^2+mb^2\dot{\theta}^2$$
$$\Rightarrow \dot{\theta}=\frac{\theta}{R}\sqrt{GM_e\frac{a^2-2ab}{R(a^2+b^2)}}$$
What next?

 

[voko]

First of all, I am not convinced that you got the potential energy correctly. As I said previously, the potential energy is given by $- GMm/r$, not by $GMm/r$ as you seem to have used.

Secondly, I do not see that $(4ab - 2a^2)/R^3$ follows from the expression for $U''(0)$ that you obtained.

Other than that, conservation of energy is not $U_0 = U + K$, but $U_0 + K_0 = U + K$. This is a differential equation, solving which you should get periodic motion. And determine its period, which is what you need to solve the problem.

 

[Saitama]

First of all, I am not convinced that you got the potential energy correctly. As I said previously, the potential energy is given by $- GMm/r$, not by $GMm/r$ as you seem to have used.

Secondly, I do not see that $(4ab - 2a^2)/R^3$ follows from the expression for $U''(0)$ that you obtained.

Other than that, conservation of energy is not $U_0 = U + K$, but $U_0 + K_0 = U + K$. This is a differential equation, solving which you should get periodic motion. And determine its period, which is what you need to solve the problem.

I will be correcting the equations by tomorrow, I have to leave now but isn't $K_0=0$?

 

[voko]

I will be correcting the equations by tomorrow, I have to leave now but isn't $K_0=0$?

If $U_0$ is the potential energy at the equilibrium, and $K_0$ is the kinetic energy at the same position, what does $K_0 = 0$ imply?