kingwinner
- 1,266
- 0
Theorem:
A stationary AR(1) model can be expressed in terms of MA(infinity).
Proof:
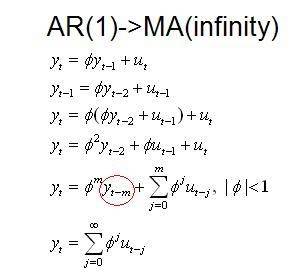
Now I don't understand how they get from the second last line to the last line. Where did the term Yt-m go?
I understand you can keep doing the substitution iteratively, but you always have to end up with a "Y" term no matter how many times you do it, but on the last line of the proof there is no "Y" term, so it magically disappared? I'm really confused.
Hopefully someone can explain this (in simple terms if possible). Thank you!
A stationary AR(1) model can be expressed in terms of MA(infinity).
Proof:
Now I don't understand how they get from the second last line to the last line. Where did the term Yt-m go?
I understand you can keep doing the substitution iteratively, but you always have to end up with a "Y" term no matter how many times you do it, but on the last line of the proof there is no "Y" term, so it magically disappared? I'm really confused.
Hopefully someone can explain this (in simple terms if possible). Thank you!