Torque and Rotational Equilibrium with a slanted Rod/Cable

[JwdePhysics]

Homework Statement

There is a lever rod of length 3.43 m, weight 44 N and uniform density. The lever rod is
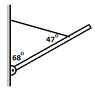
pivoted on one end and is supported by a cable attached at a point 0.902 m from the other end. The lever rod is in equilibrium at angle of 68◦ from the vertical wall. The cable makes angle of 47◦ with the rod. I want to know the tension in the cable.

Homework Equations

Since everything at equilibrium all net forces and the net torque are equal to 0.
Fnetx=Horizontal Tension-Normal Horizontal Force=0
Fnety=Vertical Tension-Normal Vertical Force-The weight=0
tNet = Torque caused by the cable- Torque caused by the rod=0

The Attempt at a Solution

Well, in order to get the horizontal and vertical forces of the tension, I need the angle that makes the altitude of a triangle from the vertex connecting the tension cable and the rod. So if we draw the altitude we now have a right triangle.
-One of the vertices in the triangle is 65 degrees since it is also a vertex in the triangle created by the lever rod, the cable, and the wall. Therefore since a triangle has 180 degrees, we subtract 68 and 47 and then get 65 as the angle for that vertex
-The other angle must be 25 since there are 180 degrees in a triangle and 180-90-65=25.

So now we can update the equations like this:
Fnetx=Tcos(25)-Nh=0
Fnety=Tsin(25)-Nv-44=0
tNet=T((L-0.902)*sin(25))-44(L/2)=0
and therefore plugging in 3.43 for L will yield
T = 44(3.43/2)/((3.43-0.902)*sin(25))
And solving for T gives out 70.63.

 

[TSny]

Hello. Welcome to PF.

Your equations for Fnetx and Fnety look correct (except for possibly the sign of the Nv term).

I don't think your torque equation is correct. First, when setting up a torque equation, you should always state the origin (axis) that you are using.

Can you explain how you got the expression 44(L/2) for the torque due to the weight? Note that the weight does not act perpendicularly to the rod.
Similarly, the use of sin(25) does not look correct for finding the torque due to T.

Can you confirm that the setup is as shown?

 

[JwdePhysics]

Hello. Welcome to PF.

Your equations for Fnetx and Fnety look correct (except for possibly the sign of the Nv term).

I don't think your torque equation is correct. First, when setting up a torque equation, you should always state the origin (axis) that you are using.

Can you explain how you got the expression 44(L/2) for the torque due to the weight? Note that the weight does not act perpendicularly to the rod.
Similarly, the use of sin(25) does not look correct for finding the torque due to T.

Can you confirm that the setup is as shown?
View attachment 218455

Yes, the setup shown above is correct, and sorry the origin axis I was using was the wall.

I got 44(L/2) for the weight because the rod weighs 44 N and from the center of the rod to the pivot point is L/2. So I guess that means I need to multiply that by cos(68)?

I multiplied the sin(25) with T in order to get the vertical component of it. Should I be multiplying it with the sin of a different angle?

 

[TSny]

Yes, the setup shown above is correct, and sorry the origin axis I was using was the wall.

Which point of the wall are you taking to be your origin for calculating torques?

I got 44(L/2) for the weight because the rod weighs 44 N and from the center of the rod to the pivot point is L/2. So I guess that means I need to multiply that by cos(68)?

No guessing.

I multiplied the sin(25) with T in order to get the vertical component of it. Should I be multiplying it with the sin of a different angle?

Review the definition of torque for a force in an arbitrary direction. For example, see http://www.sparknotes.com/testprep/books/sat2/physics/chapter10section4.rhtml

 

[JwdePhysics]

Which point of the wall are you taking to be your origin for calculating torques?

The hinge on which the rod pivots is the point I used for the origin.

Review the definition of torque for a force in an arbitrary direction. For example, see http://www.sparknotes.com/testprep/books/sat2/physics/chapter10section4.rhtml

Oh, so the board is like the radius and the force is like the cable, which in that case, the angle should be 47,not 25.

 

[TSny]

The hinge on which the rod pivots is the point I used for the origin.Oh, so the board is like the radius and the force is like the cable, which in that case, the angle should be 47,not 25.

Yes.

 

[JwdePhysics]

Oh oops, it should be sin of 68 not cos, and thanks for the help!

 

[TSny]

OK. Good.