maxhell
- 3
- 1
- Homework Statement
- Torque and rolling
- Relevant Equations
- Torque=Ia and F=ma
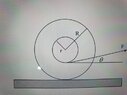
Hello,
i have tried to calculate the acceleration (COM) of the cylinder (even though in the question they asked about the angular acceleration) and the answer is:
𝑎(𝑐𝑜𝑚)=𝐹(𝑟/𝑅−𝑐𝑜𝑠(𝑡ℎ𝑒𝑡𝑎))/(𝐼/𝑅2+𝑀)
and my answer is with minus (I/R^2 - M) . in their solution they wrote in the torque equation--> f(static)R-Fr=Ia(Com)/R but i don't understand why , because the magnitude of a(com) is positive ( chose the right direction as positive) and f(static)-Fr is <0 so why take f(s)R-Fr and not like i did Fr-f(s)R=I(a(com)/R
(at b))
why isn't obvious that the cylinder will roll rightward?
thanks for the help
https://ibb.co/QPYKG3p https://ibb.co/MMTzRtS
i have tried to calculate the acceleration (COM) of the cylinder (even though in the question they asked about the angular acceleration) and the answer is:
𝑎(𝑐𝑜𝑚)=𝐹(𝑟/𝑅−𝑐𝑜𝑠(𝑡ℎ𝑒𝑡𝑎))/(𝐼/𝑅2+𝑀)
and my answer is with minus (I/R^2 - M) . in their solution they wrote in the torque equation--> f(static)R-Fr=Ia(Com)/R but i don't understand why , because the magnitude of a(com) is positive ( chose the right direction as positive) and f(static)-Fr is <0 so why take f(s)R-Fr and not like i did Fr-f(s)R=I(a(com)/R
(at b))
why isn't obvious that the cylinder will roll rightward?
thanks for the help
https://ibb.co/QPYKG3p https://ibb.co/MMTzRtS