Torque Problem: Finding the weight of a horizontal bar

[DracoMalfoy]

Homework Statement

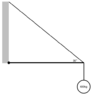
n the diagram below, the horizontal bar has a length of 4m. The force due to the wire angled at 30 degrees is 1200N. What is the weight of the horizontal bar?

Homework Equations

T=F⊥r

The Attempt at a Solution

I know that I need to add the three( the bar, the wire, and weight, but I'm not sure how to do that. I tried...

0= Tbar+Twire+Tweight
0= -Tbar+-Twire+-Tweight
0= Tsin30+-1200sin30+-400sin30⋅9.8

I'm not sure if I did this correctly. The options for answers are

A) 6640N
B) 1600N
C) 3320N
D) 4200N
E) 2750N

The first answer that i got using another method was 3320. That was wrong.

 

[gneill]

Are you sure that the force due to the wire (presumably its tension) is 1200N? Is there possibly a zero missing?

 

[DracoMalfoy]

Are you sure that the force due to the wire (presumably its tension) is 1200N? Is there possibly a zero missing?

Thats what the question states. but i think that I've found the answer. hopefully.

0=1200sin30⋅4-400⋅9.8⋅4+Tsin30⋅4
0=2400-15680+2T
-2T=-13289
T=6640

 

[haruspex]

0=1200sin30⋅4-400⋅9.8⋅4+Tsin30⋅4

I don't understand this equation. The last term appears to be the same as the first but with T standing for the tension of 1200N. Where does the weight of the bar feature?

 

[gneill]

I don't see why there would be two terms with components that depend upon the angle of the wire. Both the bar and ball have forces that point straight down (gravity).

If I look at just the weight of the ball, $400~kg \cdot g = 3923~N$, then no component of a 1200 N tension could counteract that. That's why I suspect that the given tension is suspect.

 

[DracoMalfoy]

I don't see why there would be two terms with components that depend upon the angle of the wire. Both the bar and ball have forces that point straight down (gravity).

If I look at just the weight of the ball, $400~kg \cdot g = 3923~N$, then no component of a 1200 N tension could counteract that. That's why I suspect that the given tension is suspect.

So the question is flawed? lol

 

[gneill]

So the question is flawed? lol

It happens more often than is generally comfortable

Try the tension at 12000 N and see if a one of the given answers results.

 

[J Hann]

Thats what the question states. but i think that I've found the answer. hopefully.

0=1200sin30⋅4-400⋅9.8⋅4+Tsin30⋅4
0=2400-15680+2T
-2T=-13289
T=6640

I agree with this answer.
Your method of balancing torques is interesting - I mean the term (Tsin30⋅4).
Usually, one would include the force at the pivot point of the bar and then eliminate this
force when balancing the translational forces.
You have apparently done this indirectly.

 

[gneill]

I agree with this answer.
Your method of balancing torques is interesting - I mean the term (Tsin30⋅4).
Usually, one would include the force at the pivot point of the bar and then eliminate this
force when balancing the translational forces.
You have apparently done this indirectly.

Disagree. Forces at the pivot point do not contribute to torques.

 

[haruspex]

Your method of balancing torques is interesting - I mean the term (Tsin30⋅4).

It still does not make sense to me (see post #4).
As @gneill has posted, the tension should be 12000N. With the data as given the answer is negative!

 

[CWatters]

+1

The 400kg ball is hanging from the beam by a rope. The tension in that rope is around 4000N so the tension in the main rope must be >4000N.