Torque required to lift a given mass around a point.

[Daz50]

Homework Statement

Dear Physics Forums, I was hoping you may be able to help with a problem I am having in my final postgraduate project.

A short background of the project to put the problem into context - I am designing and manufacturing a form of powered orthosis to help a person move from a sitting position to a standing position.

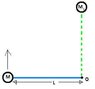
I am currently trying to calculate the forces involved in the sit-to-stand tranition. For simplicity at this stage, my image shows a very basic model I created of a mass on the end of a moment arm.

The attached file shows an image of this simple model.

The mass, M (90kg) is designed to represent a person's bodyweight, the length L (65.8cm) is the buttock-knee length of a person and the pivot point O, represents the knee joint. Anything below the knee is disregarded at this stage. The mass M is required to travel 90degrees in 1.5 seconds, finishing at M1 (the green dashed line) assuming a constant angular velocity. It is also on a vertical plain as this is supposed to model someone standing up.

Homework Equations

Torque = I Alpha (The equation I think I should be using but I am not sure how)

Torque = mass x Alpha x L² (The equation I actually used but I think is wrong)

The Attempt at a Solution

My working so far is as follows:

1) convert 90degrees into radians 90 / (pi/2) = 1.575 radians

2) Work out how many radians per second 1.575 radians / 1.5 seconds = 1.05r/s

3) Factor in the mass M, and the length, L into the equation.

90kg x 1.05rad/s x 0.658m² = 40.9Newton Metres.

I have a calculated value of 40.9Newton metres to move the 90kg mass through 90degrees, however I am not sure how to factor the effects of gravity into this equation as this would certainly have an impact on the torque required to move M to M1.

Apologies if this post is a bit all over the place - I do not have a physics background because I came from a different undergrad degree discipline so am trying my best!

Any assistance would be appreciated!

Kind regards,

Daz

 

[Villyer]

A torque causes angular acceleration (alpha).
Hence if you want constant angular velocity, your torque would be zero.

A person sitting has no angular velocity, so in order to stand they have to use their muscles to produce a torque on their leg that accelerates it to some angular velocity, and then decelerates it back to stationary when the person is upright. I guess this can be done either through the natural torque produced by gravity, or by a torque produced my your muscles on the other side of your leg. Having muscles stop you is a more precise way of doing it, since the torque produced by them isn't constant and can be adjusted.

 

[Daz50]

Hi Villyer,

Thanks for clarifying a few things. Obviously I don't want the person to have no angular velocity - otherwise they're staying sitting!

I agree with you though about the stopping method. There is some counter activation by the opposing muscles (the hamstrings) according to my research so it makes sense to suggest that they play a role in bringing the legs to a stop. As well as the natural joint range of the knee.

Could you suggest a rudimentary way to model this?

Thanks,

Daz

 

[Villyer]

The first step would be to figure out how you want the leg to move.
I would map out over what angles you want to be accelerating, when angles you want to use constant angular velocity, and when you plan on decelerating.