Torque and rotation around a fixed point

[spacediver]

This isn't a real homework problem (i.e. I made this problem up myself for my own purposes), but I figured this is the correct forum to post. 1. Homework Statement

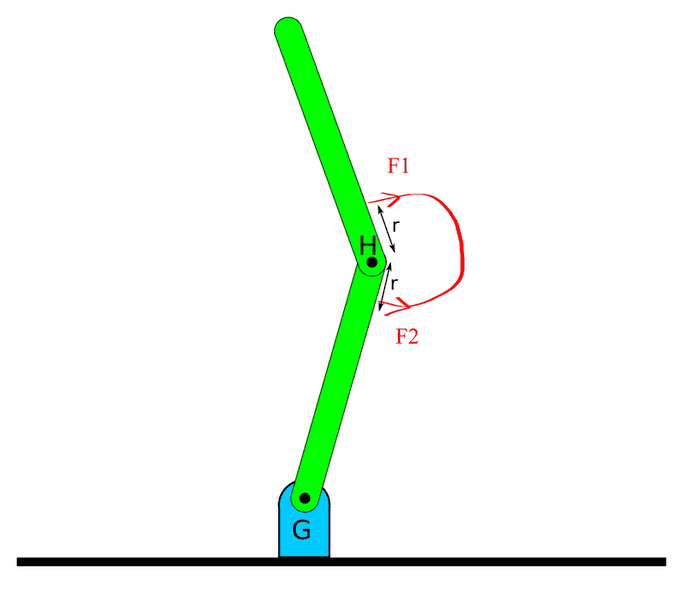
In the following figure we have two rods connected to each other, and the bottom rod is connected to the blue structure (G), and G is connected to a large immovable object. The rods can rotate around point H, and the bottom rod can rotate around the joint it creates with G.

Assume that the rods are of equal length, and are uniformly weighted.

Suppose gravity doesn't exist for the purposes of this question.

There is a muscle fiber that connects the rods. My question is this:

When the muscle fiber contracts, and exerts tension at the attached points on both rods, what happens to the system? In particular, what happens to point H? Assume F1 and F2 are directed perpendicular to each rod, and are of equal magnitude.

Homework Equations

Force = mass * acceleration
Torque = perpendicular force component * distance between fulcrum and force application
Moment of inertia of rods = 1/3 Mass*length^2
Angular acceleration due to torque = Moment of inertia/Torque

The Attempt at a Solution

[/B]
I understand that if these two segments weren't connected to G, then one could calculate the position of point H by taking advantage of the fact that the centre of mass does not change, since all the forces are internal. In that case, you would first calculate the centre of mass. Then you could calculate the torque, due to each force around point H, calculate the angular acceleration of each rod around point H, and then using geometry, one could figure out where point H is as the rods rotate around point H, since the centre of mass does not change.

But in the illustrated example, I don't think things are as straightforward.

F1 creates a clockwise torque in the top rod around H.
F2 creates a counterclockwise torque in the bottom rod around point H
F2 also creates a clockwise torque in the bottom rod around G.

And this is where my mind gets stuck. I'm not as interested in the precise answer, as I am in understanding how to approach such a problem. I'd like to be able to learn how to think about this sort of problem, and would appreciate and guidance.

 

[haruspex]

You describe the connecting string as a muscle fibre. The forces shown on the fibre clearly do not balance, so the fibre must also be in contact with something else. In the obvious interpretation of the system as an arm, that something would be connected to the joint H, not to the ground. That being so, there is a force leftwards on H.

G exerts an unknown force on the mechanism, but no torque. It follows that there can be no angular momentum change. If the two rods are the only masses, they must have equal and opposite rotation at all times.
Can you figure out from that how the rods move?

 

[spacediver]

You describe the connecting string as a muscle fibre. The forces shown on the fibre clearly do not balance, so the fibre must also be in contact with something else.

Ah, my error. If I'm understanding correctly, to depict them as balanced, the forces must be parallel to each other if they are equal in magnitude, and in my illustration they are not parallel.

In the obvious interpretation of the system as an arm, that something would be connected to the joint H, not to the ground.

I designed the system like this to simplify a conceptual problem I'm working on. The muscle fiber in question represents the glutes, the upper rod represents the torso, the lower rod represents the legs (thigh and shank represented as one rod, so I'm ignoring the knee joint), and the blue section represents the foot, connected to the ground with friction. I was trying to figure out if the contraction of the glutes could bring the hips forward (i.e. point H moving leftwards). Based on your response, I take it that the answer is yes.

G exerts an unknown force on the mechanism, but no torque. It follows that there can be no angular momentum change. If the two rods are the only masses, they must have equal and opposite rotation at all times.
Can you figure out from that how the rods move?

This is really interesting. I do see how the rods would move, given what you've said. I'm not able to grasp why G doesn't exert a torque anywhere though.

Would the situation change if the forces were applied at a different angle relative to the rods? For example, if F1 was directed more downward (so instead of the F1 vector pointing at 2:30 on a clock face as it is in the illustration, it was pointing at 3:30). That way, there would be a component of that force that was transmitted through the axes of both rods, and this would be met with a reaction force at G. Could such a reaction force at G result in a torque anywhere?

Or is the idea that because G is immobile, it cannot cause a tendency for the system to rotate about any point (as such a rotation would necessitate movement of point G itself). So no matter what magnitude or direction the resultant force of G upon the system, no torque can be expressed anywhere?

Thanks for the reply :)

 

[haruspex]

to depict them as balanced, the forces must be parallel to each other if they are equal in magnitude,

No, that wasn't my point. The muscle fibre itself must be in balance, but you only show the two forces on it. In practice, there must be another force to the right from the middle of the joint onto the muscle.

I'm not able to grasp why G doesn't exert a torque anywhere though.

I should have been more precise. It cannot exert a torque about itself as axis (because it is a free joint).

 

[CWatters]

The image here...
https://drichardsonptblog.files.wordpress.com/2016/06/force-couple.jpg?w=295&h=298
suggests to me that you model should look more like this...

 

[spacediver]

No, that wasn't my point. The muscle fibre itself must be in balance, but you only show the two forces on it. In practice, there must be another force to the right from the middle of the joint onto the muscle.

Hmm, I don't follow (but I want to). Are you suggesting that another force is required to maintain its curved shape? Or that the rods must exert an equal and opposite force onto the muscle at the two attachment points? If the latter, I left those out as I didn't think them relevant to the problem. Am I missing something fundamental here?

I should have been more precise. It cannot exert a torque about itself as axis (because it is a free joint).

I tried looking up the definition of a free joint, but couldn't find one. Can the other joints in the illustration exert torques about themselves?

The image here...
https://drichardsonptblog.files.wordpress.com/2016/06/force-couple.jpg?w=295&h=298
suggests to me that you model should look more like this...

Yes, that is more accurate. I wanted to abstract the situation into a toy problem. I like your rendition better as it allows the depiction of the contractile element (muscle fiber) as a straight line. Thanks for taking the time and effort to modify the image.

In your version, I take it that the angular momentum of the system still can't change, but that because there is an asymmetry in the mass distribution between the two rods, the rate of rotation of each rod won't be equal and opposite as they were before. Would your rendition create any other important differences?

 

[CWatters]

I didn't mean to change the mass of either rod. They could both still have the same mass and moment of inertia if you like. You could also draw it with two identical rods and a torsion spring at H (http://img.directindustry.com/images_di/photo-g/15174-2439519.jpg) The point is that a the muscles create a torque between the two rods at point H.

 

[spacediver]

Understood, and I like the torsion spring idea.

 

[haruspex]

Are you suggesting that another force is required to maintain its curved shape?

Yes. If you consider your original diagram from the muscle's point of view the only forces on it go to the left. Clearly there must be another force on it. The only place that force can come from is the joint, which means that the muscle is exerting a force to the left on the middle of the joint.
Anyway, CWatters' redrawing of the muscle as a straight line gets around the problem.

 

[spacediver]

Yes. If you consider your original diagram from the muscle's point of view the only forces on it go to the left. Clearly there must be another force on it. The only place that force can come from is the joint, which means that the muscle is exerting a force to the left on the middle of the joint.
Anyway, CWatters' redrawing of the muscle as a straight line gets around the problem.

oh, my original diagram was just implying that the muscle fiber was stiff enough to maintain its curved shape without any force to support it. But I think I see your point.

With CWatters' redrawing, I take it point H will still move leftward, as angular momentum must be conserved.

As for point G being a free joint, and thus unable to exert torque, I *think* I'm beginning to understand. The idea is that it can rotate freely without friction, and thus any torque generated by the muscle upon joint G will not "react" with point G and thus will not create a reactionary torque. If point G was fixed, and couldn't rotate, then only the top rod would be able to rotate around point H, and if that were the case, angular moment wouldn't be conserved, which must mean than an external torque was applied to the system. And the only way that could happen is via a reactionary torque from G.

Is my thinking clear here?

A related question. If G exerts a force along the axis of the bottom rod (directed to point H), wouldn't that create a clounterclockwise torque around the centre of mass of the upper rod?

 

[haruspex]

stiff enough to maintain its curved shape

Still not my point. I assume you are regarding the muscle as very light. Whatever its shape, if all the forces on it act to the left it will accelerate enormously to the left. The forces on the muscle must balance.

If G exerts a force along the axis of the bottom rod (directed to point H), wouldn't that create a clounterclockwise torque around the centre of mass of the upper rod?

Yes, there will be a torque about the mass centre of the two rod system. That is why I clarified my original comment.

With CWatters' redrawing, I take it point H will still move leftward, as angular momentum must be conserved.

When considering moments and angular momenta, it is important to be clear about the axis. The joint G cannot exert a torque about itself, so angular momentum about G is conserved. Angular momentum about other axes need not be conserved.

 

[spacediver]

Still not my point. I assume you are regarding the muscle as very light. Whatever its shape, if all the forces on it act to the left it will accelerate enormously to the left. The forces on the muscle must balance.

So muscle fiber pulls on rod in a rightward direction (green arrows in my drawing).
In reaction to this, the rod pulls leftward on muscle (not shown).
This reaction force would cause the muscle to accelerate to the left (just as if I pulled on something, i'd pull myself towards it).
The fact that the muscle isn't accelerating towards the rod means that the rod must be counteracting this acceleration. Doesn't this same situation apply in Cwatters' version?

Yes, there will be a torque about the mass centre of the two rod system. That is why I clarified my original comment.

When considering moments and angular momenta, it is important to be clear about the axis. The joint G cannot exert a torque about itself, so angular momentum about G is conserved. Angular momentum about other axes need not be conserved.

Ah, I see. Joint G cannot exert a torque about itself because the distance between the force application (of G) to the fulcrum (which is point G) is zero.

This means that if the bottom rod were to rotate counterclockwise around G, then the top rod would have to rotate clockwise around point H in order to conserve the momentum around point G (i.e. if the angular momentum around G started at 0, then contraction of muscle would not be able to change this value).

The stumbling block I'm having is that I find it hard to visualize how the bottom rod can rotate counterclockwise around G without an external force. What would be the most proximal cause of this? Surely something would have to create a counterclockwise moment around point G, and I feel that the only thing that could do this would be, for example, something yanking leftwards on the left side of the bottom rod, and that something would have to be connected to the ground.

 

[haruspex]

The fact that the muscle isn't accelerating towards the rod means that the rod must be counteracting this acceleration. Doesn't this same situation apply in Cwatters' version?

In CWatters' drawing, there are two equal and opposite forces on the muscle.

Joint G cannot exert a torque about itself because the distance between the force application (of G) to the fulcrum (which is point G) is zero.

Yes. A fixed joint can exert both a linear force and a torque, but a free joint can only exert a linear force.

This means that if the bottom rod were to rotate counterclockwise around G, then the top rod would have to rotate clockwise around point H in order to conserve the momentum around point G

Yes.

how the bottom rod can rotate counterclockwise around G without an external force.

The two rod system cannot gain angular momentum about G, but the two rods can exert torques (about G) on each other.

 

[spacediver]

In CWatters' drawing, there are two equal and opposite forces on the muscle.

Ah, right. I see this now.

The two rod system cannot gain angular momentum about G, but the two rods can exert torques (about G) on each other.

I think I can see one way this could happen in Cwatters' drawing. The muscle force pulling on the upper rod in the 7 o'clock direction is not perpendicular to the section of the rod it's attached to. Therefore, there is a component of force that is transmitted through that section of the rod (8 o'clock direction). And that force component creates a counter clockwise moment around G.

You've been extremely patient and helpful in guiding my understanding, and I'm grateful. I have one last question. Do you know of any software where I can create such systems, and introduce forces like the one in my example, and have the result simulated so I can see what happens?

 

[haruspex]

In Cwatters' drawing. The muscle force pulling on the upper rod in the 7 o'clock direction is not perpendicular to the section of the rod it's attached to. Therefore, there is a component of force that is transmitted through that section of the rod (8 o'clock direction). And that force component creates a counter clockwise moment around G

Right.

Do you know of any software where I can create such systems, and introduce forces like the one in my example,

Sorry, can't help with that.

 

[CWatters]

There is/was a free Windows program called Phun that allowed you to play around with systems like this. It was originally for fun but people built surprisingly complicated machines using it.

The wiki..
https://en.wikipedia.org/wiki/Phun
suggests it's now..
https://en.wikipedia.org/wiki/Algodoo

There are some vide on youtube.

 

[spacediver]

oh wow, that looks great, thanks!

 

[spacediver]

Here's a video in Algodoo I just created showing the hips moving leftwards due to tension between the two sections (gravity is removed).

 

[spacediver]

When considering moments and angular momenta, it is important to be clear about the axis. The joint G cannot exert a torque about itself, so angular momentum about G is conserved. Angular momentum about other axes need not be conserved.

I've been thinking about this more. I understand that G cannot exert a torque at G. But why can't G experience a net torque due to the forces in the muscle (or spring)?

After all, the system does rotate about G, so there must be a torque at G.

I guess this is another way of asking how angular momentum can be conserved around G, when there is a net torque around G.

(sorry for the thread revival, wish I had thought of this question a month ago!)