Torques on a vertical wheel due to 3 masses spaced along the wheel rim

[paulimerci]

Homework Statement

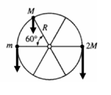
A wheel of radius R and negligible mass is mounted on a horizontal frictionless axle so that the wheel is in a vertical plane. Three small objects having masses m, M, and 2M, respectively, are mounted on the rim of the wheel, as shown. If the system is in static equilibrium, what is the value of m in terms of M ?

Relevant Equations

Rotational equilibrium:
T = F × r × sinθ. T = torque. F = linear force. r = distance measured from the axis of rotation to where the application of linear force takes place.

Applying rotational equilibrium at the center pivot we get:
+mg(R) + Mg(Rcos60°)–2Mg(R) = 0.Using cos60° = ½ we arrive at the answer 3M/2

I don't understand why cosine is used instead of sine in the above equation. I see the y component mg is acting perpendicular to the x component and so from the equation of Torque we understand that the force perpendicular to "r" is taken into consideration. I would really appreciate if anyone could explain.

 

[Orodruin]

Please post the image. We cannot help you unless we have the appropriate problem statement.

 

[paulimerci]

Thanks, I forgot to insert the picture. I've just uploaded it for your reference .

 

[haruspex]

There are two ways to think of it:
1. R x the component of Mg perpendicular to R, $RMg\cos(60)$
2. Mg x the component of R perpendicular to Mg, $MgR\cos(60)$
Where do you disagree?

 

[paulimerci]

Thanks, I find it hard visualizing it.
Why sin 60 is not used in the equation?

 

[kuruman]

Why sin 60 is not used in the equation?

What is the x-component of the radius from the center to mass $M$? Is it $R\cos(60^o)$ or $R\sin(60^o)$?

 

[paulimerci]

Well its R cos 60.

 

[paulimerci]

What is the x-component of the radius from the center to mass $M$? Is it $R\cos(60^o)$ or $R\sin(60^o)$?

While calculating torque for m, which is to the left we take it as sin 90 and thereby for calculating M which is at the top of the circle why cannot we take that as sin 60?

 

[TSny]

from the equation of Torque we understand that the force perpendicular to "r" is taken into consideration.

What is the value of the angle $\theta$ shown in the figure above? How would you use that to find the component of the force perpendicular to $r$?

 

[paulimerci]

Theta is 60. The angle between r and F is 30. I will resolve F into x and y components. Y component is parallel to r and x component looks perpendicular to r. Was it right?

 

[Lnewqban]

Welcome @paulimerci !

No need to complicate a simple concept that always works:

“The lever arm is defined as the perpendicular distance from the axis of rotation to the line of action of the force.”

The above useful statement to memorize has been copied from:
http://hyperphysics.phy-astr.gsu.edu/hbase/torq.html#torq

Please, also see:
http://hyperphysics.phy-astr.gsu.edu/hbase/torq2.html#tc

What is the value of the lever arm for the weight force of M?

 

[paulimerci]

Thank you all

View attachment 316304

What is the value of the angle $\theta$ shown in the figure above? How would you use that to find the component of the force perpendicular to $r$?

Thank you TSny! This diagram helped me to figure it out.

 

[paulimerci]

Welcome @paulimerci !

No need to complicate a simple concept that always works:

“The lever arm is defined as the perpendicular distance from the axis of rotation to the line of action of the force.”

The above useful statement to memorize has been copied from:
http://hyperphysics.phy-astr.gsu.edu/hbase/torq.html#torq

Please, also see:
http://hyperphysics.phy-astr.gsu.edu/hbase/torq2.html#tc

What is the value of the lever arm for the weight force of M?

Thanks.

 

[jack action]

T = F × r × sinθ.

The angle $\theta$ in that equation is the angle between the vectors $F$ and $r$. (reference)

In your case, it's 30° (= 90° - 60°) and sin30° = ½, just like cos60°.