Torque on Left Foot of Man in Rotating System

[KDPhysics]

Homework Statement

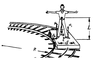
A man of mass M stands on a railroad car that is rounding an unbanked turn of radius R at speed v. His center of mass is height L above the car, and his feet are a distance d apart. How much weight is on each of his feet?

Relevant Equations

Torque equation

I saw that the solution states that the torque about the center of mass is zero, since the man does not rotate about its center of mass.
However, I then thought about taking the torque about the left foot (so the right foot for the man's POV). Hence:
$$\tau_{left} = \tau_{0} + \textbf{R}\times \textbf{F}$$
where $\textbf{R}$ is the vector pointing from the left foot to the center of mass, $\tau_{0}$ is the torque about the center of mass (so zero) and $\textbf{F}$ is the net force on the man.Then:
$$N_R d - Mg\frac{d}{2}= 0 + \textbf{R}\times \textbf{F} \implies N_R=\frac{Mg}{2} + \frac{LMv^2}{Rd} $$
which is correct. However, I wrote that the torque about the left foot is $\frac{d}{2}(2N_R-Mg)$, but clearly the man isn't rotating so shouldn't it be equal to zero? Then I would get that $N_R = \frac{Mg}{2}$. So why isn't the torque about the left foot zero.

EDIT: thinking about it, perhaps this might have to do with the fact that the left foot is not an inertial frame of reference, and that therefore we have to take into consideration the centrifugal force acting on the man. Then. I find that:
$$\tau_{left}=N_R d - Mg\frac{d}{2} - L\frac{Mv^2}{R}$$
which when equated to zero gives the desired result. But then, is my previous method (where I wrote $\tau_{left} = \frac{d}{2}(2N_R-Mg)$ incorrect?

 

[Lnewqban]

Any free body diagram with magnitudes and directions of forces as described in the problem?
The problem asks you about weight, which direction is vertical.
The weight distribution can only be between 50/50 and 100/0.
The centripetal effect tries tipping the man over and induces horizontal reactive forces at the feet, but the man is not skidding either.

 

[KDPhysics]

The weight distribution can only be between 50/50 and 100/0.

The solution to the problem (given by the book) is $N_R=\frac{Mg}{2} + \frac{LMv^2}{Rd}$, so it is not a 50/50 nor a 100/0 distribution of weight.

 

[Lnewqban]

What happens after the curve ends and R becomes infinite?
Isn't the term $2L/d$ the cotangent of the angle formed between the horizontal and vertical forces acting upon the center of mass?

 

[KDPhysics]

the railroad is circular so the curve never ends

 

[Lnewqban]

the railroad is circular so the curve never ends

OK then.
What happens to the normal reaction on outside foot when $mv^2/R$
(centrifugal force/weight) ratio equals $d/2L$ ratio?

 

[KDPhysics]

it doesn't make sense since $\frac{d}{L}$ is unitless whereas $\frac{mv^2}{R}$ has units Newtons.

 

[KDPhysics]

For anyone interested, I believe I have found an answer to my question. It turns out that the formula I suggested:
$$\tau_{left} = \tau_{0} + \textbf{R}\times \textbf{F}$$
is only correct when "left" is an inertial frame of reference. If instead we choose a point P that is accelerating, so that it is not inertial, then:
$$\frac{d\textbf{L}_P}{dt}=\tau_{ext, P} - \underbrace{M(\textbf{R}_{CM}-\textbf{R}_P)\times \ddot{\textbf{R}}_P}_{\text{pseudo-force torque}}$$
where $\textbf{L}_P$ is the angular momentum about P, and $\tau_{ext, P}$ is the net external torque about P, and $\textbf{R}_{CM}-\textbf{R}_P$ is just the vector displacement between P and the center of mass.

In the previous exercise, we have that $\frac{d\textbf{L}_P}{dt}=0$, so:
$$0 = Mg\frac{d}{2} + N_R d - L\frac{Mv^2}{R} \implies N_R = =\frac{Mg}{2} + \frac{LMv^2}{Rd}$$
as was found previously.

So, in conclusion, just because the object is not rotating about a moving point P does not mean that the net torque about P is zero, since the pseudo-force torque must be taken into account. The only exception is when the moving point is the center of mass, in which case the pseudo-force torque is zero ($\textbf{R}_{CM}-\textbf{R}_P = 0$) and therefore the the net torque is also zero.

 

[hutchphd]

The weight distribution can only be between 50/50 and 100/0.

not a 50/50 nor a 100/0

I believe @Lnewqban did not say "either/or". He said "in the range between". I think you are talking past each other!

 

[KDPhysics]

I believe @Lnewqban did not say "either/or". He said "in the range between". I think you are talking past each other!

Oh, that makes much more sense...

 

[KDPhysics]

I believe @Lnewqban did not say "either/or". He said "in the range between". I think you are talking past each other!

also is the explanation I posted correct? I think it makes sense but you never know.

 

[hutchphd]

Lets look at some limits: v=0 looks right, R gets large looks right, d gets large looks right, Units good. I think it is correct

 

[KDPhysics]

great!