Transfer function of AC Transformer

[Lord Doppler]

Homework Statement

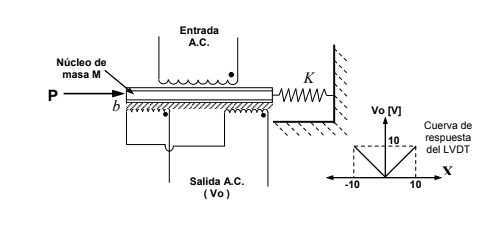
For the following system you will find its transfer function Vo (s) / P (s). East
system produces a voltage signal as a function of the applied gauge pressure
at the core of a Linear Variable Differential Transformer (LVDT), which
supplies an A.C. voltage of magnitude proportional to the displacement of the nucleus.
(Only consider positive displacements.)

Relevant Equations

P= F/A
Friction force = bx'

I'm solving this exercise, first I did a force diagram for the transformer nucleus and I got this:

∑Fx = ma
P(t) - Fk - Fb = ma
P(t) = mx''+ bx' + kx

So I got that dynamic equation, my question is, after transform that dynamic equation to Laplace Domain how can I relate it with the Output Voltage, I'm not sure, I obtain this:

X(s)/P(s) = 1/ms^2 + bs + k

And I need Vo(s)/P(s)

Thank you for your support

 

[DaveE]

The output voltage (AC) is just proportional to the displacement. Since they said only consider positive displacement, you can ignore the sign change at zero; you're only operating on one side of that graph. So, the output voltage is just a constant times the displacement x, as shown in the graph. You will have to do the inverse transform to solve for x, assuming you want the output voltage in the time domain. But they only asked for the s domain, so you're answer lies in the graph that shows the relationship between x and v.

 

[Lord Doppler]

The output voltage (AC) is just proportional to the displacement. Since they said only consider positive displacement, you can ignore the sign change at zero; you're only operating on one side of that graph. So, the output voltage is just a constant times the displacement x, as shown in the graph. You will have to do the inverse transform to solve for x, assuming you want the output voltage in the time domain. But they only asked for the s domain, so you're answer lies in the graph that shows the relationship between x and v.

So, the relation I found, Vo = mX like you said, then X=Vo / m. I only replace X in the transfer function I got first?
I obtain that Vo(s)/P(s) = m / Ms^2 + bs + k ; where m is the slope of the graph and M the mass of the transformer nucleus, is correct?