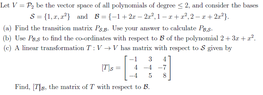Transition Matrix: Polynomial to Coordinate Form

[Kaspelek]

Hi guys,

I'm having a little difficulty in converting a set of two bases into a transition matrix. My problem lies in the bases, because they are in polynomial form compared to your elementary coordinate form.

How would I go about finding the transitional matrix for this example...View attachment 824

Thanks in advance guys (Cool)

 

[Fernando Revilla]

We have $$-1+2x-2x^2=(-1)1+(2)x+(-2)x^2\\1-x+x^2=(1)1+(-1)x+(1)x^2\\2-x+2x^2=(2)1+(-1)x+(2)x^2$$ Transposing we get $$P_{\mathcal{S},\mathcal{B}}=\begin{bmatrix}{-1}&{\;\;1}&{\;\;2}\\{\;\;2}&{-1}&{\color{red}-1}\\{-2}&{\;\;1}&{\;\;2}\end{bmatrix}\;,\quad P_{\mathcal{B},\mathcal{S}}=\begin{bmatrix}{-1}&{\;\;1}&{\;\;2}\\{\;\;2}&{-1}&{\color{red}-1}\\{-2}&{\;\;1}&{\;\;2}\end{bmatrix}^{-1}=\ldots$$

 

[Kaspelek]

We have $$-1+2x-2x^2=(-1)1+(2)x+(-2)x^2\\1-x+x^2=(1)1+(-1)x+(1)x^2\\2-x+2x^2=(2)1+(-1)x+(2)x^2$$ Transposing we get $$P_{\mathcal{S},\mathcal{B}}=\begin{bmatrix}{-1}&{\;\;1}&{2}\\{\;\;2}&{-1}&{1}\\{-2}&{\;\;1}&{2}\end{bmatrix}\;,\quad P_{\mathcal{B},\mathcal{S}}=\begin{bmatrix}{-1}&{\;\;1}&{2}\\{\;\;2}&{-1}&{1}\\{-2}&{\;\;1}&{2}\end{bmatrix}^{-1}=\ldots$$

shouldn't the matrix be =\begin{bmatrix}{-1}&{\;\;1}&{2}\\{\;\;2}&{-1}&{-1}\\{-2}&{\;\;1}&{2}\end{bmatrix}

 

[Kaspelek]

shouldn't the matrix be =\begin{bmatrix}{-1}&{\;\;1}&{2}\\{\;\;2}&{-1}&{-1}\\{-2}&{\;\;1}&{2}\end{bmatrix}

Anyway, I've worked out the inverse matrix to be

|1 0 -1|
|2 -2 -3|
|0 1 1 |

I'm not sure about how to do parts b and c)

I'm thinking that perhaps for part b) you multiply with respect to that new basis?

 

[Barioth]

Hi for b) I would try to write the polynomial in a vector of basis S. Once this is done, you could try multiplying it with one of the P matrix you have found (I'm try to find out with one!) altough you could also just play with it and find the new vector in basis B,

but doing so, you wouldn't learn much!

For c) The matrix given is in basis S how could you change it?! I leave this one to you, if you complete the b) you should be able to deal with this one :)

 

[TheBigBadBen]

shouldn't the matrix be =\begin{bmatrix}{-1}&{\;\;1}&{2}\\{\;\;2}&{-1}&{-1}\\{-2}&{\;\;1}&{2}\end{bmatrix}

Anyway, I've worked out the inverse matrix to be

|1 0 -1|
|2 -2 -3|
|0 1 1 |

I'm not sure about how to do parts b and c)

I'm thinking that perhaps for part b) you multiply with respect to that new basis?

So to be sure, you were right about the typo in the matrix Fernando Revilla had. Having computed the inverse as necessary, your next step would be to say

$$[v]_\mathcal{S} = P_{\mathcal{S},\mathcal{B}} [v]_\mathcal{B}\\
= \begin{bmatrix}{1}&{\;\;0}&{-1}
\\{2}&{-2}&{-3}
\\{0}&{\;\;1}&{1}\end{bmatrix}\,
\begin{bmatrix}{2}
\\{3}
\\{1}\end{bmatrix}
$$

For c), the necessary computation is
$$[T]_{\mathcal{B}} =
P_{\mathcal{B},\mathcal{S}} \,
[T]_{\mathcal{S}} \,
P_{\mathcal{S},\mathcal{B}} $$
Each of which you have previously computed.