mattt
- 299
- 125
humbleteleskop said:
With constant velocity magnetic field is constant.
Are you serious or just trolling? :-)
The discussion revolves around the propagation of electric and magnetic fields in free space, specifically in the context of a charged sheet accelerating and maintaining a constant velocity. Participants explore the implications of Maxwell's equations, particularly regarding the behavior of electric and magnetic fields under these conditions.
Participants express disagreement on the nature of the magnetic field generated by a charged body moving at constant velocity, with some asserting it has time dependence while others maintain that it can be treated as static under certain conditions. The discussion remains unresolved regarding the implications of these differing views.
Participants highlight limitations in applying certain laws, such as the Biot-Savart Law, to scenarios involving moving charges, indicating that assumptions about current and field behavior may not hold in all cases.
humbleteleskop said:
With constant velocity magnetic field is constant.
mattt said:Are you serious or just trolling? :-)
mattt said:I meant that even using "his" Biot-Savart formula for that situation, \vec{B}(x,y,z,t) depends explicitly on time.
humbleteleskop said:@Born2bwire
I don't see you calculated B field, what am I supposed to compare mine to? Are we even talking about the same thing? I'm not really sure if what you call "field" is the same thing I call "field potential". Don't they have different units in your and my equations?
humbleteleskop said:@Born2bwire
I don't see you calculated B field, what am I supposed to compare mine to? Are we even talking about the same thing? I'm not really sure if what you call "field" is the same thing I call "field potential". Don't they have different units in your and my equations?
Born2bwire said:I don't know what a field potential is. Fields and potentials are two different things. A potential is the kernel for the resulting field. We all have only been discussing the electromagnetic field. Nobody has used the phrase "field potential" except yourself and it is obvious from the equations that you post that you are talking about the field.
Our units are the same. Going into the magnetic field is superfluous at this point as we first need to discuss whether or not you understand what is wrong with your expression for the electric field (though matt has already given you the non-relativistic magnetic field for a similar case). Besides, the electric field defines the electromagnetic field in this case via Maxwell's Equations. So once we correct the electric field, we will have the correct magnetic field as a result.
You keep treating the electron like it is stationary in space. Your electromagnetic field states that no matter where the electron lies, the field is infinite at the origin. It takes into no account where the electron is at any point in time nor where the observer lies. Surely you understand that the Coulombic field is centered at the location of the electron, not at the origin of the coordinate system?
humbleteleskop said:Can you express that magnetic field with either some equation or numerically, or not?
.
mattt said:Dude, it is the formula you cited (the Biot-Savart approximate formula for the Magnetic FIELD created by a point charge moving with velocity \vec{v} ) :
\vec{B} = \frac{\mu_0}{4\pi}\frac{q}{r^3} \vec{v}\times\vec{r}
That is a VECTOR FIELD, not a potential anything...
humbleteleskop said:So our equations are the same, what are we arguing about then?
How to call it? It is generally a type of vector field, yes, but in the case of EM fields they are more precisely referred to as "field potentials". You gave us the equation for magnetic field potential and I'll give us the equation for electric field potential.
http://en.wikipedia.org/wiki/Electric_potential
-"In classical electromagnetism, the electric potential (a scalar quantity denoted by Φ, ΦE or V and also called the electric field potential or the electrostatic potential) at a point of space is the amount of electric potential energy that a unitary point charge would have when located at that point. "
Whether that is the same thing you call "field", that I don't know.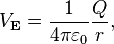
mattt said:\vec{B} is NOT the magnetic vector potential, neither the scalar magnetic potential.
Born2bwire said:You have been giving us the fields, what you just quoted above is the electric potential and that is not what you have been giving us in your equations made obvious by the fact that the units are different and that the electric potential is a scalar, not a vector.
And no, your magnetic field equation is not what we have derived.
Again, do you understand why your electric field equation is not correct compared to the electric field that I gave you?