- #1
mindarson
- 64
- 0
Homework Statement
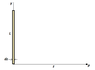
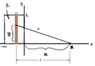
Consider a uniformly charged, infinitesimally thin rectangular sheet with total charge Q extending from x = 0 to x = -w and from y = 0 to y = L. Find the electric field at an arbitrary distance x along the positive x-axis.
Homework Equations
Superposition; E = ∫kdq/r2
The Attempt at a Solution
The picture shows how I'm approaching this problem. In the integral, 'dR' just means I'm doing a double integral over the rectangular region labeled R. I've pulled the charge density σ out of the integral, since the problem states it is uniform, therefore constant.
The confusion I'm having is that I need a pair of variables to integrate with respect to over the rectangular region. THEN I need to express the distance r in terms of those variables, so that I can actually do the integral. Since the region I'm integrating over is rectangular, I'd like to use typical x and y as variables, and I already have the limits of integration for those variables. BUT I haven't been able to express the distance, r, from source point to my point on the positive x-axis in terms of the variables x and y. I tried to use trig but that just seems to confuse things.
Finally, I don't know if this is important or not, but I haven't been able to find a way to account for that bit of horizontal distance on the left side of the y-axis, i.e. what would be the x-coordinate of the vector from the origin to my (arbitrary) source point. If I could find an expression for that, then maybe I could just use Pythagoras's Theorem to get an expression for r in terms of x and y?
Can anyone offer any pointers?
Last edited by a moderator: