Tricky Spring-Mass Problem (Vibrations)

[Saladsamurai]

This is for a vibrations course. A force F(t)=F_ocos(w*t) is applied to a point on a spring located 25% of its length from the fixed end (at the ceiling).

I am trying to write out Newton's 2nd for the block. This requires that I find how much of F(t) is transmitted to the block.

I am a little confused as to where to start.

I am also confused as to why they labeled the different parts of the spring with different spring constants? (see figure below from solution) Why do different parts of the spring have different constants. Is k a function of length?

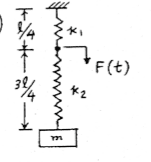
Any ideas are appreciated.

 

[Astronuc]

Spring constant is determined by the material and dimensional characteristics, e.g. wire diameter and its pitch (coils/unit length), so two springs could have different spring constants, k1 and k2.

In this problem the driving or excitation force is applied at the joint between the two springs.

One has to determine the equations of motion for each spring. It is a coupled system.

Does one consider the spring masses?

Are l/4 and 3l/4 the equilibrium lengths of the springs?

 

[Saladsamurai]

Spring constant is determined by the material and dimensional characteristics, e.g. wire diameter and its pitch (coils/unit length), so two springs could have different spring constants, k1 and k2.

In this problem the driving or excitation force is applied at the joint between the two springs.

One has to determine the equations of motion for each spring. It is a coupled system.

Does one consider the spring masses?

Are l/4 and 3l/4 the equilibrium lengths of the springs?

They are not two separate springs. It is one spring with a force applied .25L from the ceiling.

Mass of spring = 0

I am thinking that I should make a 'cut' at the point where F(t) is being applied.
I will call that point P and draw a free-body diagram.

I am confused as to how to determine the magnitude of the forces acting on P.
They both oppose the motion at all times (that is, they are negative).

One is a result of the top 25% is spring and one from the bottom .75%

And L is the length of the spring when the mass is at equilibrium.

 

[Astronuc]

One could write two equations using k1 = k2 = k. The response depends on the phase betwen F(t) and mg, which is affected by the frequency of the excitation force and the natural fequency of the spring.