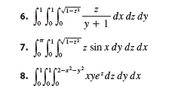Triple Integral: $\dfrac{\sqrt{1-x^2}}{2(1+y)}$

[karush]

View attachment 9379
ok this is a snip from stewards v8 15.6 ex
hopefully to do all 3 here

$\displaystyle\int_0^1\int_{0}^{1}\int_{0}^{\sqrt{1-x^2}}\dfrac{z}{y+1} \,dxdzdy$
so going from the center out but there is no x in the integrand

$\displaystyle\int_0^{\sqrt{1 - x^2}} \dfrac{z}{y + 1}dx =\dfrac{ \sqrt{1 - x^2} z}{y + 1}$
and

$\displaystyle\int_0^1 \dfrac{ \sqrt{1 - x^2} z}{y + 1} \, dz=\frac{\sqrt{1-x^2}}{2\left(1+y\right)} $

kinda maybe so far?

 

[topsquark]

ok this is a snip from stewards v8 15.6 ex
hopefully to all 3 here

$\displaystyle\int_0^1\int_{0}^{1}\int_{0}^{\sqrt{1-x^2}}\dfrac{z}{y+1} \,dxdzdy$
so going from the center out but there is no x in the integrand

$\displaystyle\int_0^{\sqrt{1 - x^2}} \dfrac{z}{y + 1}dx =\dfrac{ \sqrt{1 - x^2} z}{y + 1}$
and

$\displaystyle\int_0^1 \dfrac{ \sqrt{1 - x^2} z}{y + 1} \, dz=\frac{\sqrt{1-x^2}}{2\left(1+y\right)} $

kinda maybe so far?

You've got it! Keep going...

-Dan

Addendum: Actually, no. You've got a typo. That first (inside) integral has an upper limit of [math]\sqrt{1 - z^2}[/math], not [math]\sqrt{1 - x^2}[/math]. But you've got the idea down.

 

[karush]

$\displaystyle\int_0^1\int_{0}^{1}\int_{0}^{\sqrt{1-z^2}}\dfrac{z}{y+1} \,dxdzdy$
so going from the center out but there is no x in the integrand

$\displaystyle\int_0^{\sqrt{1 -z^2}} \dfrac{z}{y + 1}dx =\dfrac{ \sqrt{1 - z^2} z}{y + 1}$
and

$\displaystyle\int_0^1 \dfrac{ \sqrt{1 - z^2} z}{y + 1} \, dz=\frac{\sqrt{1-x^2}}{2\left(1+y\right)} $wait I think I ? on this z thing...

 

[topsquark]

$\displaystyle\int_0^1\int_{0}^{1}\int_{0}^{\sqrt{1-z^2}}\dfrac{z}{y+1} \,dxdzdy$
so going from the center out but there is no x in the integrand

$\displaystyle\int_0^{\sqrt{1 -z^2}} \dfrac{z}{y + 1}dx =\dfrac{ \sqrt{1 - z^2} z}{y + 1}$
and

$\displaystyle\int_0^1 \dfrac{ \sqrt{1 - z^2} z}{y + 1} \, dz=\frac{\sqrt{1-x^2}}{2\left(1+y\right)} $wait I think I ? on this z thing...

Take it step by step. You've got this.
[math]\int_0^1 \dfrac{z \sqrt{1 - z^2}}{y + 1} dz = \dfrac{1}{y + 1} \int_0^1 z \sqrt{1 - z^2} ~ dz[/math]

Now do a trig substitution...

-Dan