- #1
Contadoren11
- 11
- 0
Hi,
Two questions.
1) I'm having trouble understanding the stability of the stable Lagrangian points (L_4 and L_5); Wikipedia explains that if an object in the L_4 or L_5 of a planet is pushed closer towards the common center of gravity of the Sun and the planet, the increased speed that comes from a reduced distance to the center of gravity (due to conserved angular momentum) compensates for this (and the other way around (i.e. if it's pushed farther from the center of gravity)). I don't understand it intuitively nor can I explain it physically. Anyone care to have a go explaining it? Google seems to yield nothing.
2) I don't understand this formula that gives the eccentricity of an orbit expressed by the specific mechanical energy of the object (assuming orbit around the Sun, so virtually a one-body problem):
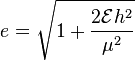
Intuitively, it makes sense to me that the eccentricity would vary depending on the mechanical energy, but I can't understand the presence of the h^2, nor how (or indeed if at all) the value of h^2 would change if, say, the speed (and thus mechanical energy) of an object in orbit were to suddenly increase, for instance. Again, anyone feel like having a go at explaining to me how the formula makes sense? (Also, am I correct in assuming that the lowest possible energy for an object in orbit would result in a circular orbit, while the eccentricity would gradually increase with mechanical energy?)
Oh, and the bottom paragraph of this site confuses me even more, as it states that the mechanical energy and e aren't connected (the way I understand it): http://courses.physics.northwestern.edu/Phyx125/Orbital%20Stuff.pdf
Any help is much appreciated (my lack of comprehension frustrates me greatly...)
Two questions.
1) I'm having trouble understanding the stability of the stable Lagrangian points (L_4 and L_5); Wikipedia explains that if an object in the L_4 or L_5 of a planet is pushed closer towards the common center of gravity of the Sun and the planet, the increased speed that comes from a reduced distance to the center of gravity (due to conserved angular momentum) compensates for this (and the other way around (i.e. if it's pushed farther from the center of gravity)). I don't understand it intuitively nor can I explain it physically. Anyone care to have a go explaining it? Google seems to yield nothing.
2) I don't understand this formula that gives the eccentricity of an orbit expressed by the specific mechanical energy of the object (assuming orbit around the Sun, so virtually a one-body problem):
Intuitively, it makes sense to me that the eccentricity would vary depending on the mechanical energy, but I can't understand the presence of the h^2, nor how (or indeed if at all) the value of h^2 would change if, say, the speed (and thus mechanical energy) of an object in orbit were to suddenly increase, for instance. Again, anyone feel like having a go at explaining to me how the formula makes sense? (Also, am I correct in assuming that the lowest possible energy for an object in orbit would result in a circular orbit, while the eccentricity would gradually increase with mechanical energy?)
Oh, and the bottom paragraph of this site confuses me even more, as it states that the mechanical energy and e aren't connected (the way I understand it): http://courses.physics.northwestern.edu/Phyx125/Orbital%20Stuff.pdf
Any help is much appreciated (my lack of comprehension frustrates me greatly...)
Last edited by a moderator: