- #1
- 2,386
- 4
Ok, I'm having trouble understanding the path-homotopy equivalence class. It's kind of blurry when they apply the operation...
[f]*[g] = [f*g]
...where [f] is the path-homotopy equivalence class of f.
I can see that an element in [f]*[g] is in [f*g], but not the other way around.
For example, if f is a path from x0 to x1 and g from x1 to x2, then f*g is a path from x0 to x2. This means that [f*g] is the equivalence class of f*g with paths from x0 to x2.
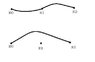
But take a look at the picture I got. We have a path on the bottom from x0 to x2 without crossing x1, but how does that fit into [f]*[g]?
What's going on here?
[f]*[g] = [f*g]
...where [f] is the path-homotopy equivalence class of f.
I can see that an element in [f]*[g] is in [f*g], but not the other way around.
For example, if f is a path from x0 to x1 and g from x1 to x2, then f*g is a path from x0 to x2. This means that [f*g] is the equivalence class of f*g with paths from x0 to x2.
But take a look at the picture I got. We have a path on the bottom from x0 to x2 without crossing x1, but how does that fit into [f]*[g]?
What's going on here?