Telemachus
- 820
- 30
Hi there. I have some trouble with this problem, it asks me to find the Fourier expansion series for the function
f(t)=0 if -pi<t<0, f(t)=t^2 if 0<t<pi
So I've found the coefficients a_0=\displaystyle\frac{1}{\pi}\displaystyle\int_{0}^{\pi}t^2dt=\displaystyle\frac{\pi^2}{3}
a_n=\displaystyle\frac{1}{n^2}\cos(n\pi)
b_n=-\displaystyle\frac{\pi\cos(n\pi)}{n}-\displaystyle\frac{4}{n^3\pi}
Then the Fourier series expansion:
f(t)\sim{\displaystyle\frac{\pi^2}{6}+\sum_{n=1}^{\infty}\displaystyle\frac{1}{n^2}\cos(n\pi)\cos(nt)- \left( \displaystyle\frac{\pi}{n}+ \displaystyle\frac{4}{n^3\pi}\right)\sin(nt)}
When I plot this on mathematica I get something that doesn't look like what I'm looking for. I've tried many ways, I've done the integrals first by hand, then I did it with mathematica, the graph always seems the same, it doesn't get to zero in the interval zero to -pi as it should, and it isn't close to the plot of t^2, it doesn't even get to zero on the origin. I don't know what I'm doing wrong. I've looked at the equations carefully, I'm pretty much sure I've done things right. Whats happening?
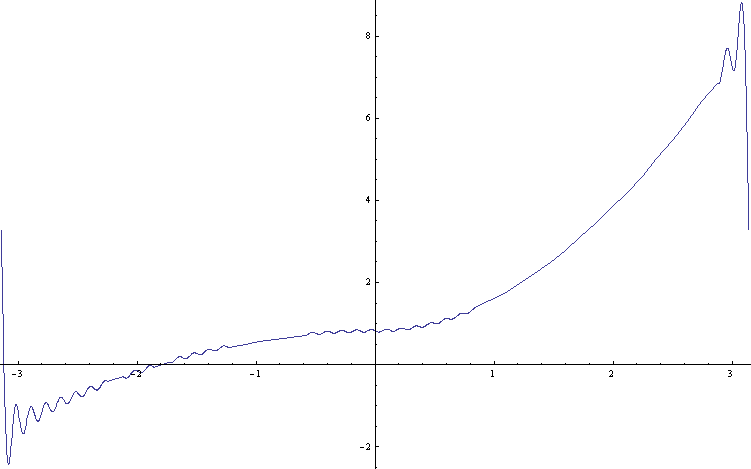
I've also tried to make a distinction between the odd and even cases, but as I supposed it didn't affect at all, the equation as I wrote it includes both cases.
f(t)=0 if -pi<t<0, f(t)=t^2 if 0<t<pi
So I've found the coefficients a_0=\displaystyle\frac{1}{\pi}\displaystyle\int_{0}^{\pi}t^2dt=\displaystyle\frac{\pi^2}{3}
a_n=\displaystyle\frac{1}{n^2}\cos(n\pi)
b_n=-\displaystyle\frac{\pi\cos(n\pi)}{n}-\displaystyle\frac{4}{n^3\pi}
Then the Fourier series expansion:
f(t)\sim{\displaystyle\frac{\pi^2}{6}+\sum_{n=1}^{\infty}\displaystyle\frac{1}{n^2}\cos(n\pi)\cos(nt)- \left( \displaystyle\frac{\pi}{n}+ \displaystyle\frac{4}{n^3\pi}\right)\sin(nt)}
When I plot this on mathematica I get something that doesn't look like what I'm looking for. I've tried many ways, I've done the integrals first by hand, then I did it with mathematica, the graph always seems the same, it doesn't get to zero in the interval zero to -pi as it should, and it isn't close to the plot of t^2, it doesn't even get to zero on the origin. I don't know what I'm doing wrong. I've looked at the equations carefully, I'm pretty much sure I've done things right. Whats happening?
I've also tried to make a distinction between the odd and even cases, but as I supposed it didn't affect at all, the equation as I wrote it includes both cases.
Attachments
Last edited: