Michael Nelo
- 3
- 0
The Problem
So, I know the basic, the basic differential equation of movement in terms of the angle it is formed, which has the form: 0 = g⋅sin[α(t)] + α''(t)⋅l. However, I decided to consider the friction force of the air, which is always contrary to the movement, and proportional to the tangential velocity, the expresion I get is this one:

So I thought maybe I could use some of the methods from homogeneous linean differential equations, but it doesn't (or at least I think it doesn't) fulfill the requirements, because the variable that isn't derivated is in a Sin().
What I have tried
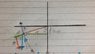
I used the usual Consideration of Forces, using an X and Y plane supportive towards l⋅Cos(θ) and l⋅Sin(θ) respectively as can be seen from the picture:

So doing the respective analysis I found said weird differential equation, here's the full process of it:

Then, I went and used the Conservation of Energy, to try and get a expression of θ'(t) to be a function of θ(t), so here's what I got:

Doing this process:

And while yes, I achieved to reduce the weird differential equation to one that doesn't involve θ'(t), the expresion just gets weird, it isn't as easily solved as the would-be equation without the friction force of the air.
What I wish to know, and What I'm going to do
I wish to know if the concepts and analytical expressions I've used are correct (for example, is the velocity used in the kinetic energy the tangential one? If no, then must I take it to be the norm of the vector →v, which includes normal and tangential velocities? If so, would I be better off just including the vectorial components?), as well as any kind of tip I can get to solve the differential equation. For this problem as well, I'm going to try to use parametric equations as well, taking advantage that the pendular movement depicts a trayectory of a circumference, I could use the canonic equation of a circumference, then derivate it regarding to time, and see what I can get.
So, I know the basic, the basic differential equation of movement in terms of the angle it is formed, which has the form: 0 = g⋅sin[α(t)] + α''(t)⋅l. However, I decided to consider the friction force of the air, which is always contrary to the movement, and proportional to the tangential velocity, the expresion I get is this one:
So I thought maybe I could use some of the methods from homogeneous linean differential equations, but it doesn't (or at least I think it doesn't) fulfill the requirements, because the variable that isn't derivated is in a Sin().
What I have tried
I used the usual Consideration of Forces, using an X and Y plane supportive towards l⋅Cos(θ) and l⋅Sin(θ) respectively as can be seen from the picture:
So doing the respective analysis I found said weird differential equation, here's the full process of it:
Then, I went and used the Conservation of Energy, to try and get a expression of θ'(t) to be a function of θ(t), so here's what I got:
Doing this process:
And while yes, I achieved to reduce the weird differential equation to one that doesn't involve θ'(t), the expresion just gets weird, it isn't as easily solved as the would-be equation without the friction force of the air.
What I wish to know, and What I'm going to do
I wish to know if the concepts and analytical expressions I've used are correct (for example, is the velocity used in the kinetic energy the tangential one? If no, then must I take it to be the norm of the vector →v, which includes normal and tangential velocities? If so, would I be better off just including the vectorial components?), as well as any kind of tip I can get to solve the differential equation. For this problem as well, I'm going to try to use parametric equations as well, taking advantage that the pendular movement depicts a trayectory of a circumference, I could use the canonic equation of a circumference, then derivate it regarding to time, and see what I can get.