Truss analysis problem

[jojosg]

TL;DR: determine the internal force of member OA

Hi I'm struggling with this problem. I have calculated the angle to be 45 degrees with tan(theta) = a/a. A is a roller which only has Ay and O has Ox & Oy as a fixed pin. (see fbd.png) is my FBD correct?

 

[Lnewqban]

TL;DR: determine the internal force of member OA

Hi I'm struggling with this problem. I have calculated the angle to be 45 degrees with tan(theta) = a/a. A is a roller which only has Ay and O has Ox & Oy as a fixed pin. (see fbd.png) is my FBD correct?

In order not to have any movement or displacement in this system, the effects of both applied forces must be counteracted by those two supports, which are the only connection of that structure to the solid ground.

Therefore, your FBD should include all the ways in which those effects could reach those supports.

The directions of the forces potentially reaching each support coincide with the geometry of the connecting links, which are only able to transfer traction or compression forces.

Your FBD is missing the possible influence of links HO and HA.

 

[jojosg]

In order not to have any movement or displacement in this system, the effects of both applied forces must be counteracted by those two supports, which are the only connection of that structure to the solid ground.

Therefore, your FBD should include all the ways in which those effects could reach those supports.

The directions of the forces potentially reaching each support coincide with the geometry of the connecting links, which are only able to transfer traction or compression forces.

Your FBD is missing the possible influence of links HO and HA.

what if I take method of sections and use the left side?

 

[Lnewqban]

Please, see:
https://mathalino.com/reviewer/engineering-mechanics/method-sections-analysis-simple-trusses

https://mathalino.com/reviewer/engineering-mechanics/problem-435-transmission-tower-method-sections

 

[wrobel]

A reaction in the hinge O has two components. A reaction in the hinge A has only a vertical component. We have three unknowns. Find them first by considering the equations of equilibrium for the whole construction as a rigid bod

 

[jojosg]

A reaction in the hinge O has two components. A reaction in the hinge A has only a vertical component. We have three unknowns. Find them first by considering the equations of equilibrium for the whole construction as a rigid bod

ok for Fy=0; Oy + Ay = 2F, Fx=0; Ox + F = 0, Ma=0; 2F(2a) - Oy(2a) - F(2a) = 0; which gives Oy = F & Ay = F & Ox = -F.

 

[wrobel]

which gives Oy = F & Ay = F & Ox = -F.

I have got the same and my guess is that the internal force must be Ox

 

[Steve4Physics]

I have got the same and my guess is that the internal force [in member OA] must be Ox

That would only be true if the tension in member OH were zero. But in the x-direction, the force-balance at point O is:
$-F~ +~ T_{OA}~ +~ T_{OH} \cos 45^ \circ = 0$

 

[Steve4Physics]

what if I take method of sections and use the left side?

The way you've marked the 'cut' in your Post #3 diagram suggests that you may have misunderstood the method of sections.

A suitable cut is th red line:

Consider the section above the red line as a single object. It has known external forces at O, E and C. There are 3 additional unknown external forces on the object: $T_{AO}, T_{AB}$ and $T_{AH}$ corresponding to the tensions in members AO. AB and AH;

[EDIT. Added $O_x$ and $O_y$ to image. ]

This new object is in equlibrium. By balancing its x-forces, y-forces and moments, you can find the 3 unkown forces (one of which is the required force).

 

[wrobel]

That would only be true if the tension in member OH were zero. But in the x-direction, the force-balance at point O

yes I agree. Then the only possibility I see is to write equations of equilibrium for each rod.

 

[Steve4Physics]

yes I agree. Then the only possibility I see is to write equations of equilibrium for each rod.

The 'Method of Sections' is a way around this. See Post #9 which is intended to start the OP solving the problem using this method.

 

[jojosg]

The 'Method of Sections' is a way around this. See Post #9 which is intended to start the OP solving the problem using this method.

Like this?

 

[Steve4Physics]

Like this?

You are on the right track but it looks like you have ignored some forces when expressing $\Sigma F_x=0, ~\Sigma F_y=0$ and $\Sigma M=0$. (But see EDIT at bottom).

You found that $O_x=-F$ (i.e. F acting to the left) and $O_y = F$.

With the bottom-right section removed, the new object in equilibrium, with all of its external forces shown, is this:

(Note that $A_y$ is not needed as it was an external force acting on the section that has been removed.)

Use of $\Sigma F_x=0, ~\Sigma F_y=0$ and $\Sigma M=0$ requires that all the forces shown on the above diagram are considered.
_________________
EDIT.
Your working may well be correct but unfortunately I can't follow it in your 3 diagrams. However, your final statement ("F=0") can't be correct as F is an arbitrary external force (not the force you are required to find).

For clarity/readability, equations here should be written using LaTeX. The link to the LateX Guide appears at the bottom-left of the edit-window. Or, for convenience, here it is: https://www.physicsforums.com/help/latexhelp/

 

[jojosg]

\sum M_0 = 0
-F(2a) + A_y(2a) = 0
A_y = F

\sum F_x = 0
F + A_x = O_x

\sum F_y = 0
O_y + A_y = 2F

\sum M_A = 0
-F(2a) + 2F(2a) - O_y(2a) = 0
F = O_y

F = O_x - A_x

\sum F_y = 0
-2F - \frac{F_{OH}}{\sqrt{2}} = 0

O_x = 2F
A_x = F

Summary:
\boxed{A_y = F}
\boxed{A_x = F}
\boxed{O_x = 2F}
\boxed{O_y = F}

 

[Steve4Physics]

\sum M_0 = 0
-F(2a) + A_y(2a) = 0
A_y = F

\sum F_x = 0
F + A_x = O_x

\sum F_y = 0
O_y + A_y = 2F

\sum M_A = 0
-F(2a) + 2F(2a) - O_y(2a) = 0
F = O_y

F = O_x - A_x

\sum F_y = 0
-2F - \frac{F_{OH}}{\sqrt{2}} = 0

O_x = 2F
A_x = F

Summary:
\boxed{A_y = F}
\boxed{A_x = F}
\boxed{O_x = 2F}
\boxed{O_y = F}

I'm out for most of today but will take a look when I return.

 

[Steve4Physics]

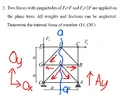
@jojosg, there are a number of issues, so it's complicated to explain. But here is an attempt...

I've written some of your equations from Post 14, so that LaTeX renders them correctly (for me anyway). This required putting a pair of hash symbols ($\# \#$) at the beginning and end of each equation.

So, the first part of your Post 14 working (with some comments aded) is this:
__________________________________

$\sum M_0 = 0$
$-F(2a) + A_y(2a) = 0$
$A_y = F$
That looks OK.
___________________________________

$\sum F_x = 0$
$F + A_x = O_x$
Not really. There is a roller at point A. There is no external horizontal reaction from a (perfect) horizontal roller. So you know in advance that $A_x=0$..

If you don’t use this fact (that $A_x=0$), then you have thrown away critical supplied information; this may prevent you from finding the correct answer.

The only 2 horizontal external forces are $O_x$ at point O and $F_1$ at point C.
___________________________________

$\sum F_y = 0$
$O_y + A_y = 2F$
That looks OK.

You already found that $A_y = F$. So it follows that $O_y=F$. You don't need your next step...
___________________________________

$\sum M_A = 0$
$-F(2a) + 2F(2a) - O_y(2a) = 0$
$F = O_y$

That's OK. but it is an unecessary step, as already noted.
___________________________________

$F = O_x - A_x$
But $A_x$ is known to be zero. See above.
___________________________________

$\sum F_y = 0$
$-2F - \frac{F_{OH}}{\sqrt{2}} = 0$
Not clear about this. It looks like you are referring to the system with a cut to remove the bottom-left section.

It appears you have assumed member GO has a tension of 2F and member AO has a tension equal to $O_x$. That's wrong.

You need to redraw your diagram to show all external forces: carefully examine the Post #13 comments and diagram.
___________________________________

Additional note.

You have marked $O_x$ on a diagram as pointing left. By convention, an unknown x-component is assumed positive (pointing right, in the +x direction). With this corrected, $O_x = -F$.

You can then (on a subsequent diagram) show this as a force F pointing left. Care is needed to avoid introducing sign-errors.

There may be other issues I've missed.

Minor edits (& again).