Trying to derive Gauss' law using a cylindrical surface

[annamal]

When I try to derive Gauss's law with a straight line of charge with density $\lambda$ through a cylindrical surface of length L and radius R,
$$\vec E = \frac{\lambda*L}{4\pi\epsilon*r^2}$$
$$A = 2\pi*r*L$$
$$\vec E*A = \frac{\lambda *L^2}{2\epsilon*r} \neq \frac{q_{enc}}{\epsilon}$$
What am I doing wrong?

 

[Doc Al]

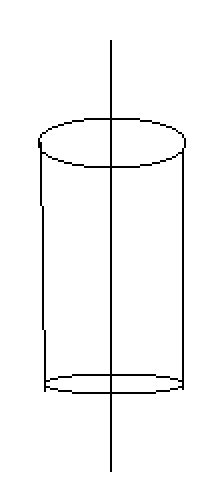
$$\vec E = \frac{\lambda*L}{4\pi\epsilon*r^2}$$

Don't confuse the field from a point charge with that of a line of charge. Look it up!

 

[vanhees71]

First of all your "syntax checker" should alarm you that you have equated a vector with a scalar!

I guess you are considering an "infinitely long" homogeneous line-charge along the $z$ axis of a cylindrical coordinate system. Now think about the symmetry of the problem, i.e., in which direction must the electric field point, and then use an arbitrary cylindrical volume, $V$, with the axis along the line-charge distribution and evaluate carefully Gauss's Law,
$$\int_{\partial V} \mathrm{d}^3 \vec{f} \cdot \vec{E}=\frac{1}{\epsilon_0} Q_V,$$
where $\partial V$ is the boundary of the cylinder (with the surface-normal vectors pointing out of this cylinder), and $Q_V$ is the charge inside the considered cylindrical volume, $V$.