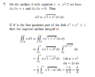JD_PM
- 1,125
- 156
Homework Statement
Homework Equations
The Attempt at a Solution
[/B]
I understand how the integral is solved using cartesian coordinates.
However, I wanted to try to solve it using polar coordinates:
$$\int_0^{\pi/2} cos \theta \sqrt{1+r^2 cos^2 \theta}d \theta\int_{0}^{\sqrt{1-r^2 cos^2 \theta}}r^3dr$$
But it doesn't seem to be a good idea.
Am I wrong or we cannot find a better method than cartesian coordinates for solving this integral?