alejandrito29
- 148
- 0
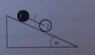
two cylinder conected, by two roads, rolling down an inclined plane. Find equation of motion and tension of roads.
I know that the lagrangian is:
0.5 m \dot{x}^2+0.5 I_1 \dot{\theta}^2++0.5 I_1 \dot{\theta}^2+mgx\sin \alpha + mg(x+l)\sin \alpha
¿ is good my lagrangian?, ¿how is present the tension of roads at the lagrangian?
I know that the lagrangian is:
0.5 m \dot{x}^2+0.5 I_1 \dot{\theta}^2++0.5 I_1 \dot{\theta}^2+mgx\sin \alpha + mg(x+l)\sin \alpha
¿ is good my lagrangian?, ¿how is present the tension of roads at the lagrangian?