Discussion Overview
The discussion revolves around the derivation and definitions of generalized forces in the context of monogenic systems, exploring the relationship between different formulations of these forces and their implications in mechanics.
Discussion Character
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants inquire about the derivation of one equation of generalized forces from another for monogenic systems.
- Definitions of the force ##F_i## in the context of generalized forces are questioned and clarified.
- One participant asserts that there are mechanical systems where the generalized force can be expressed in terms of a velocity-dependent potential, leading to a specific form of Lagrange's equation.
- Another participant expresses confusion regarding the apparent contradiction between the general definition of generalized forces and the specific form for monogenic systems.
- Some participants agree that in certain special cases, the generalized force takes a specific form, but they do not provide a definitive proof for the equivalence of the two formulations.
- Examples, such as the Lorentz force, are provided to illustrate specific cases where the generalized force can be derived from a velocity-dependent potential.
- A formula for a rigid body is introduced, relating net force and torque to generalized forces.
Areas of Agreement / Disagreement
Participants express differing views on the definitions and derivations of generalized forces, with no consensus reached on the equivalence of the general and specific forms for monogenic systems. Some participants agree on certain aspects, but the overall discussion remains unresolved.
Contextual Notes
There are limitations in the discussion regarding the assumptions made about the definitions of generalized forces and the conditions under which the specific forms apply. The mathematical steps leading to the equivalence of the two formulations are not fully resolved.

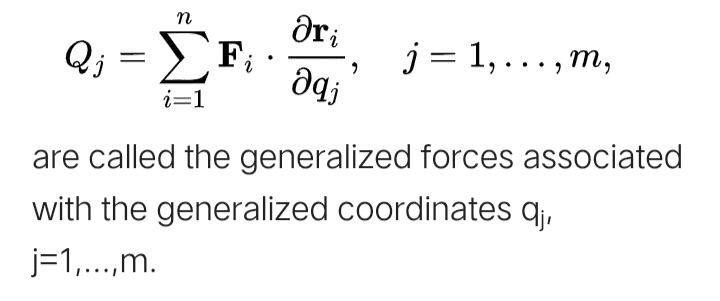 How can I derive the first equation from the second for a monogenic system ?
How can I derive the first equation from the second for a monogenic system ?