Two masses connected by a rope on a pulley on a ramp

Thread starter runningphysics
Start date Jan 29, 2022
Tags

Incline plane Mass Newton's 2nd law Normal force Pulley Ramp Rope Tension Two masses

Click For Summary

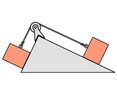
SUMMARY

The discussion focuses on solving a physics problem involving two masses connected by a rope over a pulley on a ramp. Participants emphasize the importance of using distinct symbols for each mass to avoid confusion. They recommend writing force balance equations for each mass, either by separating forces into horizontal and vertical components or by analyzing forces parallel and normal to the slope. This structured approach simplifies the problem-solving process.

PREREQUISITES

Understanding of free body diagrams
Knowledge of Newton's laws of motion
Familiarity with force balance equations
Basic concepts of inclined planes in physics

NEXT STEPS

Study how to create and interpret free body diagrams
Learn about Newton's second law in the context of multiple bodies
Research inclined plane dynamics and friction effects
Explore problem-solving techniques for pulley systems in physics

USEFUL FOR

Students studying physics, educators teaching mechanics, and anyone interested in understanding dynamics involving pulleys and inclined planes.

Jan 29, 2022

runningphysics

Homework Statement: If the left-hand slope in the figure makes a 58° angle with the horizontal, and the right-hand slope makes a 32° angle, how should the masses compare if the objects are not to slide along the frictionless slopes?

Relevant Equations: F=ma

I have no clue how to do the problem. I created a free body diagram for each block. I assume that it is simpler than I am making it out to be.

Physics news on Phys.org

Jan 29, 2022

haruspex

Science Advisor

Homework Helper

Insights Author

Gold Member

2024 Award

First, use a different symbol for each mass. Calling them both "m" will confuse.

Next, write the force balance equations for each mass.
You can write an equation for each of horizontal and vertical or for parallel to the slope(s) and normal to them. Your choice.

Thread 'Magnitude of buoyant force in fluids of different densities'

The book claims the answer is that all the magnitudes are the same because "the gravitational force on the penguin is the same". I'm having trouble understanding this. I thought the buoyant force was equal to the weight of the fluid displaced. Weight depends on mass which depends on density. Therefore, due to the differing densities the buoyant force will be different in each case? Is this incorrect?

View full post »