Kashmir
- 466
- 74
Suppose a sphere is rolling on horizontal surface. The point of contact is the instantaneous center of rotation. It's velocity momentarily is zero. So in a time dt it'll stay where it is.
However during this time dt the point next to this contact point at its right side will move forward and down, thus after time dt we will have two points in contact with the horizontal surface. Which is wrong.
What's wrong with my approach?
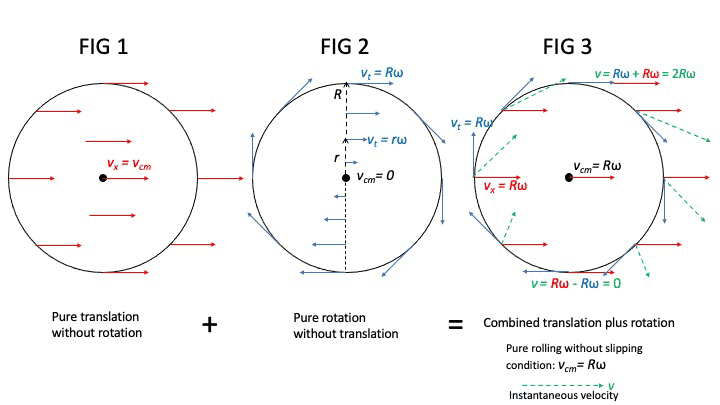
However during this time dt the point next to this contact point at its right side will move forward and down, thus after time dt we will have two points in contact with the horizontal surface. Which is wrong.
What's wrong with my approach?