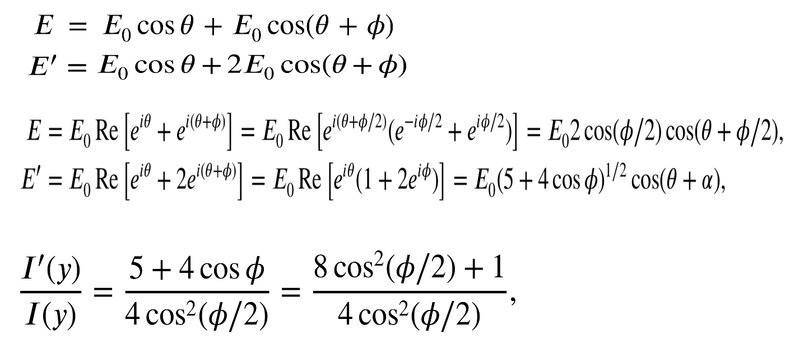Two slit interference: new intensity after doubling width

[maxim07]

Homework Statement

A 2 slit interference pattern is viewed on a screen at distance R>>d from the plane of the slits where d is the slit spacing. If y is the transverse displacement across the screen, with y = 0 corresponding to the forward direction from the centre of the slits the intensity on the screen for small y is given by I = Icos^2(y*pi*d/wR), w is wavelength

If one of the slits is made twice as wide so that the amplitude of the point source has doubled show the intensity becomes

I’ = I/4(9cos^2(y*pi*d/wR) +1)

Relevant Equations

Cos(A) + cos(B) = 2cos(A+B/2)cos(A-B/2)

Here is the solution, I understand how they got E, but I don’t see how they could get E’ from cosine addition formulas? I don’t need to know how to do it with complex numbers.

 

[haruspex]

From a little experimentation, I got that $\alpha=2\phi/3$. But when I plug that in it does not seem to work. Might be an issue with multiple solutions of $arccos(c)$.

Cracked it, @maxim07 :
$\cos(\theta)+2\cos(\theta+\phi)=\cos(\theta)+2\cos(\theta)\cos(\phi)-2\sin(\theta)\sin(\phi)$
$=\cos(\theta)(1+2\cos(\phi))-2\sin(\theta)\sin(\phi)$.
Defining $\cos(\alpha)=\frac{1+2\cos(\phi)}{\sqrt{5+4\cos(\phi)}}$ we find that $\sin(\alpha)=\frac{2\sin(\phi)}{\sqrt{5+4\cos(\phi)}}$
So $\cos(\theta)+2\cos(\theta+\phi)=(\cos(\theta)\cos(\alpha)-\sin(\theta)\sin(\alpha))\sqrt{5+4\cos(\phi)}$

 

[maxim07]

But if you didn’t know the end result where would the sqrt(5 + 4cos(φ)) come from ?

 

[TSny]

The key is to write $\cos \theta + 2 \cos (\theta + \phi)$ as one cosine expression. That is, find $A$ and $\alpha$ such that $$\cos \theta + 2 \cos (\theta + \phi) = A \cos(\theta + \alpha)$$ for all values of $\theta$.

Hint: One approach is to expand $\cos(\theta + \phi)$ on the left side of the above equation and expand $\cos(\theta + \alpha)$ on the right. Rearrange the overall equation by collecting together all terms containing $\cos \theta$ and all terms containing $\sin \theta$. Thus obtain an equation of the form $$a \cos\theta + b \sin\theta = 0$$ where $a$ and $b$ are expressions in terms of $A$, $\alpha$, and $\phi$. For this equation to hold for all possible choices of $\theta$, what can you say about $a$ and $b$?

An alternate approach is to use phasors. But, I don't know if you are familiar with this method.

 

[haruspex]

But if you didn’t know the end result where would the sqrt(5 + 4cos(φ)) come from ?

Faced with an equation like $A\sin(x)+B\cos(x)=C$ a useful trick is to let $\cos(y)=\frac A{\sqrt{A^2+B^2}}$, so $\sin(y)=\frac B{\sqrt{A^2+B^2}}$ and $\frac C{\sqrt{A^2+B^2}}=\frac A{\sqrt{A^2+B^2}}\sin(x)+\frac B{\sqrt{A^2+B^2}}\cos(x)=\cos(y)\sin(x)+\sin(y)\cos(x)$
$=\sin(x+y)$.

 

[maxim07]

The key is to write $\cos \theta + 2 \cos (\theta + \phi)$ as one cosine expression. That is, find $A$ and $\alpha$ such that $$\cos \theta + 2 \cos (\theta + \phi) = A \cos(\theta + \alpha)$$ for all values of $\theta$.

Hint: One approach is to expand $\cos(\theta + \phi)$ on the left side of the above equation and expand $\cos(\theta + \alpha)$ on the right. Rearrange the overall equation by collecting together all terms containing $\cos \theta$ and all terms containing $\sin \theta$. Thus obtain an equation of the form $$a \cos\theta + b \sin\theta = 0$$ where $a$ and $b$ are expressions in terms of $A$, $\alpha$, and $\phi$. For this equation to hold for all possible choices of $\theta$, what can you say about $a$ and $b$?

An alternate approach is to use phasors. But, I don't know if you are familiar with this method.

tanθ = -a/b ?

 

[TSny]

tanθ = -a/b ?

If you have an equation of the form $a \cos \theta + b \sin \theta = 0$, where $a$ and $b$ are independent of $\theta$, and if the equation is to hold for all $\theta$, then you can conclude that $a = 0$ and $b = 0$. For example, you can let $\theta = 0$ to get $a = 0$.

 

[maxim07]

Ah okay, so then I get 1 + 2cos Φ - Acos α= 0 and -2sin Φ + Asin α = 0

 

[TSny]

Ah okay, so then I get 1 + 2cos Φ - Acos α= 0 and -2sin Φ + Asin α = 0

Looks good. You have two unknowns: $A$ and $\alpha$. And you have two equations.

Can you eliminate $\alpha$ so that you get one equation for $A$? Hint: $\sin^2\alpha + \cos^2\alpha = 1$.

 

[maxim07]

Greta thanks solved it