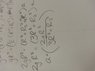Two Toilet Papers dropping-Rotational Inertia

[CentrifugalKing]

Homework Statement

Okay, so I'm supposed to take two fresh rolls of toilet paper and drop them. One of which, I am supposed to let unravel while falling. The other, I just drop on its own. I'm supposed to find the height at which both will drop and hit the ground at the same time.

Homework Equations

Rotation Inertia for Toilet Papers: I= M (R-R2)^2

Conservation of Energy: KE1 + PE1 = KE2 + PE2

The Attempt at a Solution

I know that

KE1= 0 and PE2 = 0

So

PE1 = KE2

mgh = (1/2) Iw^2 + (1/2)Mv^2

Okay... this was all I wrote. At this point I realized, that I did not know the difference between the two.

What would make the unraveling toilet paper any different from the one that falls?

 

[Doc Al]

What would make the unraveling toilet paper any different from the one that falls?

For one thing, the final PE of the unraveling toilet paper will not be zero. It stretches out as it unravels.

 

[CentrifugalKing]

Oh so it will be

mgh= (1/2)(M)(Rf)((v^2)/(Rf^2)) +Mv^2 + PE?

So what would PE equal? Would the mass change to just one sheet of paper rather than the whole roll?

Or should I also set up Newton's 2nd Law?

 

[Doc Al]

Or should I also set up Newton's 2nd Law?

That's what I would do. See if you can compare the accelerations.

 

[CentrifugalKing]

Hate to bump this up again, but I've gotten pretty far but got jumbled on one part.

So I did net torque = I(alpha)

And did some substitution

mg*R = (((1/2)(M) (R^2+R2^2) + MR^2))) (a/R)

Thing is, would

R^2+R2^2 be the same as the other R's?

Sorry if I'm not being clear. But how would the formula play out? I know M cancels.

 

[Doc Al]

Hate to bump this up again, but I've gotten pretty far but got jumbled on one part.

So I did net torque = I(alpha)

And did some substitution

mg*R = (((1/2)(M) (R^2+R2^2) + MR^2))) (a/R)

This looks good. Note: R is the outer radius; R₂ is the inner radius.

Thing is, would

R^2+R2^2 be the same as the other R's?

Not sure what you mean. See my comment above.

The linear acceleration will be in terms of both R and R₂.

 

[CentrifugalKing]

@Doc Al

Thanks for all your help, and I think I got it.

After a bit of Algebra:

(2/3)((g*R^2)/(R^2+R2^2))=a

And the other a=g

Is that all I can do?

And then compare it?

 

[Doc Al]

After a bit of Algebra:

(2/3)((g*R^2)/(R^2+R2^2))=a

I get something slightly different, so double check your algebra.

And the other a=g

Is that all I can do?

And then compare it?

Once you have the two accelerations, figure out how the heights they must be dropped from have to relate for them to fall in the same time. (Hint: for a given distance, solve for the time to reach the ground.)

 

[CentrifugalKing]

Oh,

So I did a bit.

Is this correct?

I brought the R from a/R to the other side.
I wanted to cancel the 1/2 so I multiplied everything by 2.

2gR^2 = (R^2+R2^2+2R^2) a?

 

[CentrifugalKing]

Oh I see my mistake! So this is right?

 

[Doc Al]

Oh,

So I did a bit.

Is this correct?

I brought the R from a/R to the other side.
I wanted to cancel the 1/2 so I multiplied everything by 2.

2gR^2 = (R^2+R2^2+2R^2) a?

This looks better. But simplify the expression within the parenthesis a bit--combine terms.

 

[Doc Al]

Oh I see my mistake! So this is right?

Looks good.