roshan guthey
Long drive shaft of 5 inches fits into the end fitting and is rigidly attached by the bolts. Input torque is equal to output torque as we are ignoring losses from bearing. Let's assume that the load on the shaft is equal to 3*weight. (3 g's)
(looking for more conceptual understanding rather that number crunching)
has maximum torque of let's say 1000 in-lb. with a use of material that provides max allowable stress of 10000 psi.
How would we go about drawing the deflection diagram of hallow tube?
What size bolts would be needing with same stress requirement if there were 6 bolts present?What I have so far:
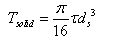
where D comes out to be 0.7985 inches. realistically speaking isn't this number is too small?
Wouldn't the the load and length affect it's diameter?
Will there is any problem if we were to create hallow shaft using equation below? But not sure what to use for first diameter. How would I draw deflection of hallow shaft?
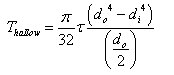
(looking for more conceptual understanding rather that number crunching)
has maximum torque of let's say 1000 in-lb. with a use of material that provides max allowable stress of 10000 psi.
How would we go about drawing the deflection diagram of hallow tube?
What size bolts would be needing with same stress requirement if there were 6 bolts present?What I have so far:
where D comes out to be 0.7985 inches. realistically speaking isn't this number is too small?
Wouldn't the the load and length affect it's diameter?
Will there is any problem if we were to create hallow shaft using equation below? But not sure what to use for first diameter. How would I draw deflection of hallow shaft?
Attachments
Last edited by a moderator: