- #1
- 1,200
- 331
This is a series of question that appear to become more and more vague, the last part has me stumped.
1. Homework Statement
A) I have an electric motor that produces 0.4 HP of shaft power at a speed of 2800rpm. What will the gearbox speed and torque be on the output of a 1:5 (in : out) gearbox? Assume a 96% efficient gearbox
B) design a shaft that is 100mm long to transmit the gearbox output torque of the above problem using sensible engineering assumptions. Select a material and design the diameter.
C) assume that you have a centrifugal pump impeller at the end of the shaft you designed in the above problem. What will be the maximum radial deflection at the tip of the centrifugal impeller with respect to the shaft? Assume that the impeller is rigid (does not deflect) and has a diameter of 100mm. Assume all deflection is from the 100mm long shaft only.
[/B]
Question A) is straight forward:
Poutput = Pin *η = 0.4HP * 0.96 = 0.384 HP
Rpmout = Rpm in * 5/1 = 14,000 RPM
HP = RPM* T / 5252
Tout = HPout*5252/RPM
= 0.386HP *5252 / 14,000 RPM = 0.1448 ft lbFor Question B), I think the simplest interpretation is "how thick must a solid shaft be to resist 0.1448 ft lb of torsion?"
I choose 316 SS (SS because it's for a pump, 316 because it's common) with yield stress of 205 MPa and a safety factor of 3.
So
0.1448 ft lb = 0.1963 Nm
τmax = 205 MPa/3 = 68.3 MPa
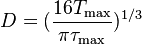 = (16x 0.1963 Nm / (π * 68.3 MPa) )1/3
= (16x 0.1963 Nm / (π * 68.3 MPa) )1/3
= 2.446 mm
Which is expectedly thin, and such a slender shaft would likely undergo whirling before 14,000rpm.
Would the next step be to find the minimum diameter that gives a critical speed beyond 14,000rpm?
That would require some assumptions about how it's supported, simply supported at both ends would be the obvious assumption.
Part C) has me stumped:
I would think the only radial stress would be due to the centrifugal force on the self weight of the shaft (and the blade weight if I estimated and included it).
Is it really asking me find the increase in radius of the shaft due to the speed of rotation?
I've only ever seen radial deflection in the context of pressure vessels & piping. I understand blade tip clearance is important but I'd assume the radial deflection of the shaft is inconsequential compared to the that of the blades themselves. Or is there some other interpretation?
1. Homework Statement
A) I have an electric motor that produces 0.4 HP of shaft power at a speed of 2800rpm. What will the gearbox speed and torque be on the output of a 1:5 (in : out) gearbox? Assume a 96% efficient gearbox
B) design a shaft that is 100mm long to transmit the gearbox output torque of the above problem using sensible engineering assumptions. Select a material and design the diameter.
C) assume that you have a centrifugal pump impeller at the end of the shaft you designed in the above problem. What will be the maximum radial deflection at the tip of the centrifugal impeller with respect to the shaft? Assume that the impeller is rigid (does not deflect) and has a diameter of 100mm. Assume all deflection is from the 100mm long shaft only.
The Attempt at a Solution
[/B]
Question A) is straight forward:
Poutput = Pin *η = 0.4HP * 0.96 = 0.384 HP
Rpmout = Rpm in * 5/1 = 14,000 RPM
HP = RPM* T / 5252
Tout = HPout*5252/RPM
= 0.386HP *5252 / 14,000 RPM = 0.1448 ft lbFor Question B), I think the simplest interpretation is "how thick must a solid shaft be to resist 0.1448 ft lb of torsion?"
I choose 316 SS (SS because it's for a pump, 316 because it's common) with yield stress of 205 MPa and a safety factor of 3.
So
0.1448 ft lb = 0.1963 Nm
τmax = 205 MPa/3 = 68.3 MPa
= 2.446 mm
Which is expectedly thin, and such a slender shaft would likely undergo whirling before 14,000rpm.
Would the next step be to find the minimum diameter that gives a critical speed beyond 14,000rpm?
That would require some assumptions about how it's supported, simply supported at both ends would be the obvious assumption.
Part C) has me stumped:
What will be the maximum radial deflection at the tip of the centrifugal impeller with respect to the shaft? Assume that the impeller is rigid (does not deflect) and has a diameter of 100mm. Assume all deflection is from the 100mm long shaft only.
I would think the only radial stress would be due to the centrifugal force on the self weight of the shaft (and the blade weight if I estimated and included it).
Is it really asking me find the increase in radius of the shaft due to the speed of rotation?
I've only ever seen radial deflection in the context of pressure vessels & piping. I understand blade tip clearance is important but I'd assume the radial deflection of the shaft is inconsequential compared to the that of the blades themselves. Or is there some other interpretation?