SUMMARY
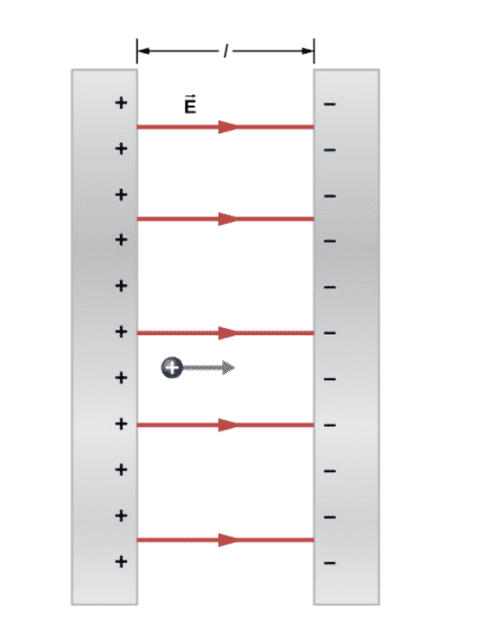
The electric field generated by a single charged plate is defined as ##E = \frac{\sigma}{2\epsilon_0}##, where ##\sigma## represents the surface charge density and ##\epsilon_0## is the permittivity of free space. When considering both a positive and a negative plate, the total electric field is not simply doubled; instead, it remains ##\vec E = \frac{\sigma}{\epsilon_0}## due to the superposition of the fields from both plates. This conclusion is derived using a pillbox Gaussian surface to analyze the electric field behavior in the vicinity of the plates.
PREREQUISITES
- Understanding of electric fields and charge distribution
- Familiarity with Gaussian surfaces and their applications in electrostatics
- Knowledge of the permittivity of free space (##\epsilon_0##)
- Basic concepts of superposition principle in physics
NEXT STEPS
- Study the application of Gaussian surfaces in electrostatics
- Explore the concept of electric field lines and their representation
- Learn about the effects of multiple charged plates on electric fields
- Investigate the relationship between surface charge density and electric field strength
USEFUL FOR
Students of physics, educators teaching electrostatics, and anyone seeking to deepen their understanding of electric fields generated by charged plates.