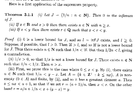Understanding Garling's Corollary 3.2.7 on Real Numbers and Rational Sequences

[Math Amateur]

I am reading D. J. H. Garling's book: "A Course in Mathematical Analysis: Volume I: Foundations and Elementary Real Analysis ... ...

I am focused on Chapter 3: Convergent Sequences

I need some help to fully understand the proof of Corollary 3.2.7 ...Garling's statement and proof of Corollary 3.2.7 (together with Proposition 3.2.6 which is mentioned in Corollary 3.2.7 ... ) reads as follows:

View attachment 9037
My questions related to the above Corollary are as follows:
Question 1

In the above proof of Corollary 3.2.7 we read the following:

" ... ... Arguing recursively, let $$r_n$$ be the 'best' rational with $$\text{max} ( x - \frac{1}{n} , r_{ n - 1 } ) \lt r_n \lt x$$ ... ... Can someone please explain (preferably in some detail) what is going on here ... how do we arrive at the expression

$$\text{max} ( x - \frac{1}{n} , r_{ n - 1 } ) \lt r_n \lt x$$ ... ... "Question 2

In the above proof of Corollary 3.2.7 we read the following:

" ... ... let $$s_n$$ be the 'best' rational with

$$x \lt s_n \lt \text{min} ( x + \frac{1}{n}, s_{ n - 1 } )$$ ... ... "Can someone please explain (preferably in some detail) what is going on here ... how do we arrive at the expression

$$x \lt s_n \lt \text{min} ( x + \frac{1}{n}, s_{ n - 1 } )$$ ... ... ?
Help will be appreciated ...

Peter==========================================================================================The post above mentions Theorem 3.1.1 and alludes to the remarks made after the proof of Theorem 3.1.1 ... so I am providing text of the theorem and the relevant remarks ... as follows:View attachment 9038
View attachment 9039

Hope that helps ...

Peter

 

[Olinguito]

Question 1

In the above proof of Corollary 3.2.7 we read the following:

" ... ... Arguing recursively, let $$r_n$$ be the 'best' rational with $$\text{max} ( x - \frac{1}{n} , r_{ n - 1 } ) \lt r_n \lt x$$ ... ... Can someone please explain (preferably in some detail) what is going on here ... how do we arrive at the expression

$$\text{max} ( x - \frac{1}{n} , r_{ n - 1 } ) \lt r_n \lt x$$ ... ... "

Garling is just trying to construct a sequence of rational numbers that is strictly increasing and converges to $x$. If $x$ itself is rational, we can just take the sequence
$$\left(x-\frac1n\right)_{n=1}^\infty$$
but $x$ might be irrational whereas we want a rational sequence. By choosing
$$\max\left(x-\frac1n,r_{n-1}\ <\ r_n\right)$$
we are ensuring that the sequence is rational and strictly increasing, and approaches arbitrarily close to $x$. Theorem 3.1.1 guarantees the existence of a strictly increasing rational sequence
$$x-1\ <\ r_1\ <\ r_2\ <\ r_3\ <\ \cdots\ <\ x$$
but we also want the $r_n$ to converge to $x$. This is done by ensuring each $r_n$ is at least $x-\dfrac1{n+1}$.

The other question is similar.

 

[Math Amateur]

Garling is just trying to construct a sequence of rational numbers that is strictly increasing and converges to $x$. If $x$ itself is rational, we can just take the sequence
$$\left(x-\frac1n\right)_{n=1}^\infty$$
but $x$ might be irrational whereas we want a rational sequence. By choosing
$$\max\left(x-\frac1n,r_{n-1}\ <\ r_n\right)$$
we are ensuring that the sequence is rational and strictly increasing, and approaches arbitrarily close to $x$. Theorem 3.1.1 guarantees the existence of a strictly increasing rational sequence
$$x-1\ <\ r_1\ <\ r_2\ <\ r_3\ <\ \cdots\ <\ x$$
but we also want the $r_n$ to converge to $x$. This is done by ensuring each $r_n$ is at least $x-\dfrac1{n+1}$.

The other question is similar.

Thanks for that helpful post ,,,

The idea of the proof is clear to me now ...

Peter