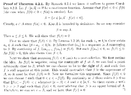Intermediate Value Theorem ....Silva, Theorem 4.2.1 .... ....

[Math Amateur]

I am reading Cesar E. Silva's book entitled "Invitation to Real Analysis" ... and am focused on Chapter 4: Continuous Functions ...

I need help to clarify an aspect of the proof of Theorem 4.2.1, the Intermediate Value Theorem ... ...

Theorem 4.2.1 and its related Corollary read as follows:
View attachment 9562
View attachment 9563
In the above proof by Silva, we read the following:

" ... ... So there exists \(\displaystyle x\) with \(\displaystyle b \gt x \gt \beta\) and such that \(\displaystyle f(x) \lt 0\) ... ... "My question is as follows:

How can we be sure that \(\displaystyle f(x) \lt 0\) given \(\displaystyle x\) with \(\displaystyle b \gt x \gt \beta\) ... indeed how do we show rigorously that for \(\displaystyle x\) such that \(\displaystyle b \gt x \gt \beta\) we have \(\displaystyle f(x) \lt 0\) ...Help will be much appreciated ...

Peter

 

[GJA]

Hi Peter,

Since $\beta<b$ and $\delta >0$, there are values of $x$ such that $|x-\beta|<\delta$ and $\beta < x< b$. The key here is to remember that $|x-\beta| <\delta$. By the continuity argument, $f(x)<0$ for all such $x$.

 

[Math Amateur]

Hi Peter,

Since $\beta<b$ and $\delta >0$, there are values of $x$ such that $|x-\beta|<\delta$ and $\beta < x< b$. The key here is to remember that $|x-\beta| <\delta$. By the continuity argument, $f(x)<0$ for all such $x$.

Thanks for the help GJA!

At first I struggled with what you meant by ... " By the continuity argument, $f(x)<0$ for all such $x$ ... "

But then I found Apostol Theorem 3.7 (Calculus Vol. 1, page 143) which reads as follows:View attachment 9565Were you indeed invoking something like what Apostol calls the sign-preserving property of continuous functions?Thanks again for your help ...

Peter

 

[GJA]

Hi Peter,

Happy to help!

I wasn't quoting that purposely, though it is true. In fact, it's essentially what the author is proving by their choice of epsilon.

What I meant was: $|f(x)-f(\beta)|<\epsilon\,\Longrightarrow\, f(x)<\epsilon + f(\beta)<0.$

Hope this helps clear up the confusion on my earlier post.