Understanding How to Solve Vector Magnitudes and Angles

[bergausstein]

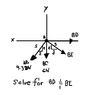
I just don't understand others way solving this problem

to solve for the unknown magnitudes of the two vectors I have to sum up all of the components in x and y and set them equal zero and from there I'll get some systems of equation.

I saw a method where they let the x-component of AB and BE to be

$\displaystyle\frac{3}{5}\cdot -9.38$ and $\displaystyle\frac{3}{5}\cdot BE$ respectively.

and the y-components of AB and BE to be

$\displaystyle\frac{4}{5}\cdot -9.38$ and $\displaystyle\frac{4}{5}\cdot -BE$ respectively

Can you explain why they do that?

and how can we solve this using angle

I know that $\arctan(\frac{4}{3})=53.1\deg$ but I'm uncertain on how to plug it in my equation properly I also know that to get the x-component I have to multiply the magnitude of the vector I'm interested into by the $\cos(53.1)$ in the problem given. but this configuration makes me wonder if I'm doing it correctly. hope you can help me with this. thanks!

 

[Ackbach]

I think some context would be good here. Is this a statics problem? I'm seeing forces on your diagram, which is typically what you find on a Free Body Diagram. If you have to set all the components equal to zero, I think you're going to have a hard time of it, as none of the vectors have any positive $y$-component.