Understanding Huffman Code and Symbol Encoding - Explained Simply

[*Jas*]

Huffman code?!?

Hi there!

Im having abit of trouble getting my head around this question concerning the Huffman code,the average length of an encoded symbol etc...

the full question is attached!...help would be v. much appreciated!

 

[HallsofIvy]

You should be aware that most people will not open a "doc" file from someone they don't know. They area notorious for having viruses.

 

[CRGreathouse]

The virus risks are overstated (that, and I'm using OOo not Word).

The problem reads:
"Consider the symbols and frequencies:
$e:0.36\;\;a:0.14\;\;d:0.26\;\;s:0.24$

(a) Find the Huffman code, and the average length of an encoded symbol.
(b) Give another prefix code for the symbols a, e, d, s. Compare the average lengths of an encoded symbol for the two codes."

So, what have you done on the problem so far? Seems straightforward enough to me.

 

[*Jas*]

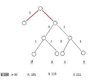
So far iv drawn the tree for the code concerned (attached image!)...however I am not sure whether it looks correct?? I am not sure about the bits in red?!?

im not sure which of the following to use:

d: 100
a: 101
s: 110
e: 111

or

e: 0.36 - 0

d: 0.26 - 10

s: 0.24 - 110

a: 0.14 - 111

 

[coventry]

dis is wrong u shuld dissconect from the site. u dnt deserve 2 be on the the website